【每日一题】初中(7-9年级)数学培优提升(第23期答案)

七

【答案】

【分析】

先根据题目中的已知条件得出此人应付的费用的代数式，再把x=8代入计算即可．

【解答】：

由题意得此人应付的费用为[12.50+2.40（x﹣3）]=2.4x+5.3 （x＞3）．

当x=8时，2.4×8+5.3=24.5（元）．

答：此人应付的费用可表示为（2.4x+5.3）元．

当x=8时，他应付的费用为24.5元．

【点评】此题考查了列代数式，关键是读懂题意，找出题目中的数量关系，根据数量关系列出代数式，要注意本题的条件．

八

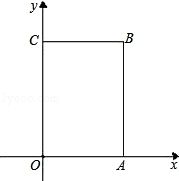
如图，长方形OABC中，O为平面直角坐标系的原点，A点的坐标为（4，0），C点的坐标为（0，6），点B在第一象限内，点P从原点出发，以每秒2个单位长度的速度沿着O﹣A﹣B﹣C﹣O的路线移动（即：沿着长方形移动一周）．

（1）写出点B的坐标（　 　）．

（2）当点P移动了4秒时，描出此时P点的位置，并求出点P的坐标．

（3）在移动过程中，当点P到x轴距离为5个单位长度时，求点P移动的时间．

【答案】

【分析】

（1）根据长方形的性质，易得P点坐标；

（2）根据题意，P的运动速度与移动的时间，可得P运动了8个单位，进而结合长方形的长与宽可得答案；

（3）根据题意，当点P到x轴距离为5个单位长度时，有P在AB与OC上两种情况，分别求解可得答案．

【解答】：

（1）根据长方形的性质，可得AB与y轴平行，BC与x轴平行；

故B的坐标为（4，6）；

（2）根据题意，P的运动速度为每秒2个单位长度，

当点P移动了4秒时，则其运动了8个长度单位，

此时P的坐标为（4，4），位于AB上；

（3）根据题意，点P到x轴距离为5个单位长度时，有两种情况：

P在AB上时，P运动了4+5=9个长度单位，此时P运动了4.5秒；

P在OC上时，P运动了4+6+4+1=15个长度单位，此时P运动了=7.5秒．

九

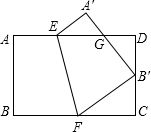
如图，将矩形纸片ABCD沿EF折叠，使点B与CD的中点重合，若AB=2，BC=3，则△FCB’与△B’DG的面积之比为()

A.9:4B.3:2C.4:3D.16:9

【答案】

D

【分析】：

设BF=x，则CF=3-x，B'F=x，在Rt△B’CF中，利用勾股定理求出x的值，继而判断△DB’G∽△CFB’，根据面积比等于相似比的平方即可得出答案．

【解答】：

设BF=x，则CF=3−x，B’F=x，

又∵点B’为CD的中点，

∴B’C=1，

在Rt△B’CF中，B’F2=B’C2+CF2，即x2=1+(3−x)2，

解得：，即可得CF=3−=，

∵∠DB’G+∠DGB’=90°，∠DB’G+∠CB’F=90°，

∴∠DGB’=∠CB’F，

∴Rt△DB’G∽Rt△CFB’，

根据面积比等于相似比的平方可得：=()2=，

故选D.