张阳:基于SOLO分类理论的数学运算分析与思考

原文发表于《中国数学教育》2021.5

开号宗旨:为数学教师提供交流、学习、研究的平台，既高中数学解题研究，也教法和学法研究。

文卫星，上海市特级教师。践行“生态课堂”，做到“两尊重”----即尊重知识的发生、发展规律，尊重学生的认知规律；把握“两个度”----思想（哲学或数学）高度和文化厚度。

在《数学教育学报》《数学通报》《中学数学教学参考》等近50家报刊杂志发表论文或文章约330多篇。

专著（代表作）：《超越逻辑的数学教学----数学教学中的德育》（2009）、《文卫星数学课赏析》（2012）、《挑战高考压轴题高中数学精讲解读篇》（1-10版，2009-2019）、《上海高考好题赏析》（2019）。

近年为北京、上海、天津、江苏、浙江、福建、广东、贵州、河南、河北、四川、云南、新疆、宁夏、安徽、山西、重庆等地师生讲学。

欢迎朋友们来稿！来稿请注明真实姓名、工作单位和联系方式。特别欢迎原创文章。只接受word版式的电子稿，文责自负。投稿邮箱：wwxwxh@163.com

作者简介：张阳，江苏泗阳人，中学高级，苏州市学科带头人，

主要研究方向，具身认知、现象教学、校本教研。

基于SOLO分类理论的数学运算分析与思考[1]

——以2020年新高考山东数学卷为例

张 阳（吴江高级中学 江苏苏州 215200）

摘要：数学运算指在明晰运算对象的基础上，依据运算法则解决数学问题的素养.2020年新高考山东数学卷按SOLO分类理论运算等级，所有试题均可按四种层次进行分析，不同层次的数学运算源于学生对问题的表征差异，而学生的学科素养水平直接影响其表征能力.在教学中，教师需要从课程标准演进中解读数学运算，在数学学科核心素养中理解数学运算，依据系统论原则培养学生数学运算.

关键词：新高考；数学运算；表征；系统；流程图

数学运算指在明晰运算对象的基础上，依据运算法则解决数学问题的素养.[1]数学运算包括算理与算法两个部分，算理指数学运算规则，如四则运算、代数式运算法则、方程与不等式的恒等变换、三角恒等变换、矩阵运算等.算法则指数学运算的方案与程序，是在算理自觉运用的前提下，与所学内容高度融合，形成某个特定问题的解题思维方法，是学生创新意识与综合能力的体现.

数学运算考查的内容主要集中在掌握运算法则、设计运算程序两个部分，前者是强调算理，后者体现算法.

一、基于SOLO分类理论的数学运算分析（以2020年新高考山东数学卷为例）

SOLO分类理论是以等级划分的形式来描述学生思维能力目标从而评价学生学习质量的一种“质性评价”方法，首先按照这一分类理论将数学运算进行层次划分，[2]见表1.

表1 试题中数学运算的SOLO层次

2020年新高考山东数学卷共22道题，除了第20题立体几何题第一问可以用逻辑推理进行证明外（考查线面垂直关系的证明，也可以通过建立空间直角坐标系，利用向量计算的方法进行证明），其余各题都需要进行数学运算.可以看出数学运算是高考数学的考查重点，作为数学学科核心素养之一，它与其它数学核心素养相互联结，共同为解题服务.

1.概念引发单一表征，考查数学运算规则（单点结构U）

问题中的概念理解没有难度，其表征形式单一，解题路径唯一，仅考查学生运算中算理能力.学生在解题时没有歧义，方法选择及运算均没有困难.

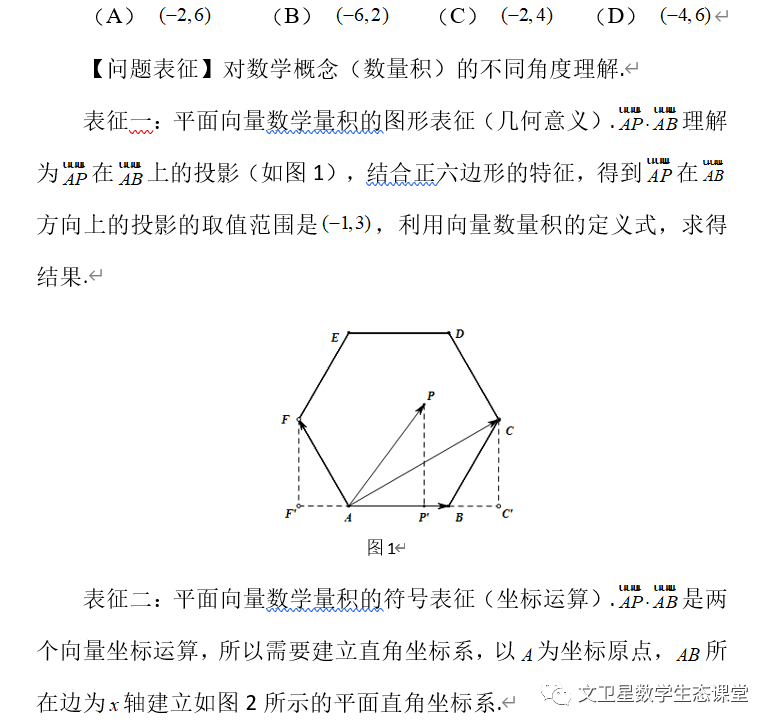
【点评】对数学问题的不同表征导致学生选择不同的运算路径.表征是指用符号、图式、动作、语言等表达数学概念或关系的行为，分为表征对象与表征结果两部分.表征既是行为也是形式，作为行为它构建了“表征”世界与“被表征”世界的对应，作为形式它在一道试题中可以有多重表征.不同的表征形式可以产生多种建模方向，直接影响到数学运算.以本题为例，从定义出发的表征，将问题转化为投影长与线段长的乘积；从运算行为出发的表征，则选择建立坐标系，转化为平面向量的坐标运算.

3.表征引发多种联想，形成不同运算方案（关联结构R）

数学问题的表征过程是理解题意的过程，自然会对问题进行内化、联想，即本题“是什么，为什么，怎么办”.

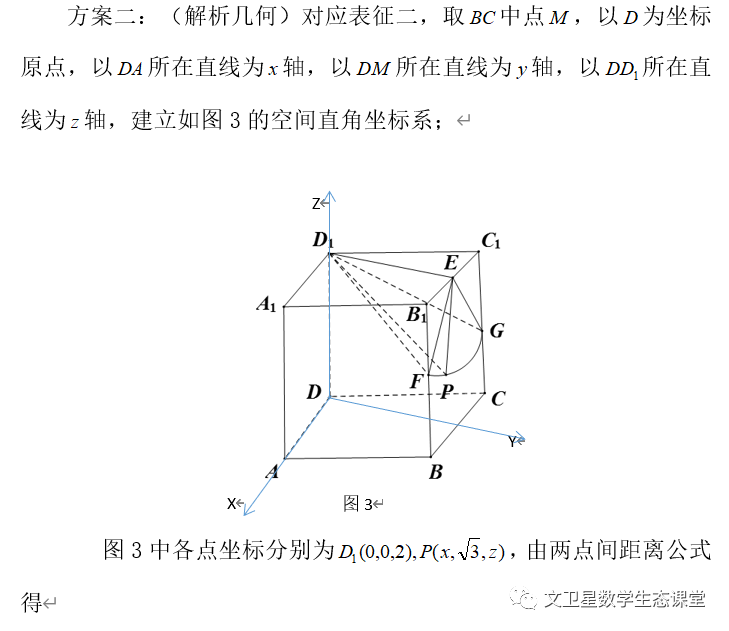
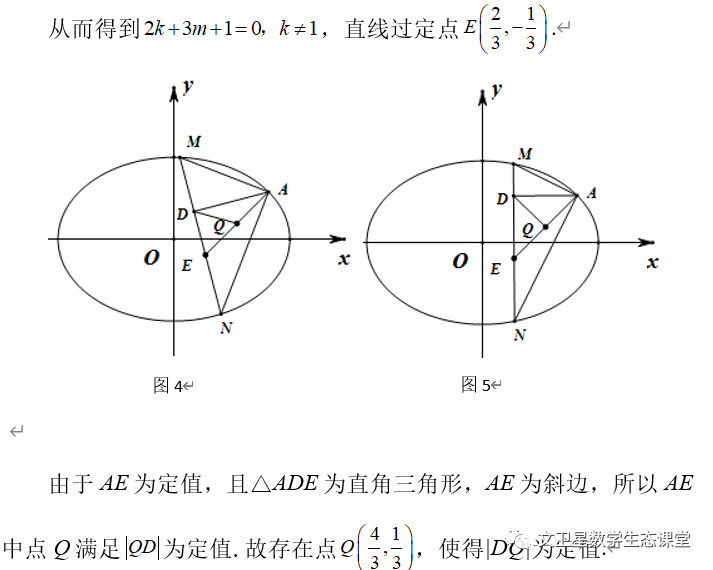
【点评】本题的两种方案都有依据，属于表征后的合理联想，但是在数学运算中算法，即运算的程序优化是解决问题的重要因素，所以数学运算不单单是计算能力，也是思维水平的体现，它的高效快捷依赖于逻辑推理、直观想象、数学建模、数学抽象、数据分析的综合应用，是学科素养的整合结果.学生的数学学科素养水平高低，映射运算方案优化程度不同.

二、关于数学运算的教学思考

数学是研究数学关系和空间形式的一门科学.数学教育承载着立德树人根本任务、发展素质教育的功能.培养学生用数学的眼光观察世界，用数学的思维分析世界，用数学的语言来描述世界，教师对数学运算的理解直接影响教学的效果与目标达成.

1.从我国课程标准演进中解读数学运算

新中国中学数学课程标准前后经历过四次系统变化，见表2.

表2 中国中学数学课程标准概要

从上表中可以看出数学运算一直是课程标准的重要组成部分，但是数学运算的内涵却发生了一定的变化，在1952年与1963年的课程标准中用计算能力来理解数学运算，即强调了数学运算中的算理部分，要求学生精通算理、准确计算；2003版的课程标准中则用运算求解能力对应数学运算，其背景是随着计算机的普及，繁琐的计算可以由计算机部分替代，课本内容随之发生变化，如开根、对数表等内容均从课本中去除，但是此时仍强调运算求解，对算理的要求大于对算法的要求；2017年的课程标准则明确将数学运算作为数学学科核心素养之一，其背景是人工智能与大数据时代的到来，对运算方案提出更高的要求，要求学生能设计算法程序，优化算法过程.

在课程标准的演进中，不难看出，数学运算从数学运算的重计算（算理）发展为重方案（算法）、重程序.

2.在数学学科核心素养中理解数学运算

数学运算是数学学科核心素养的重要组成部分，它的合理使用离不开其它五大核心素养的支撑，六个核心素养之间是相互渗透的，如数据分析与数学运算.数学核心素养在解决问题中的作用如图6.

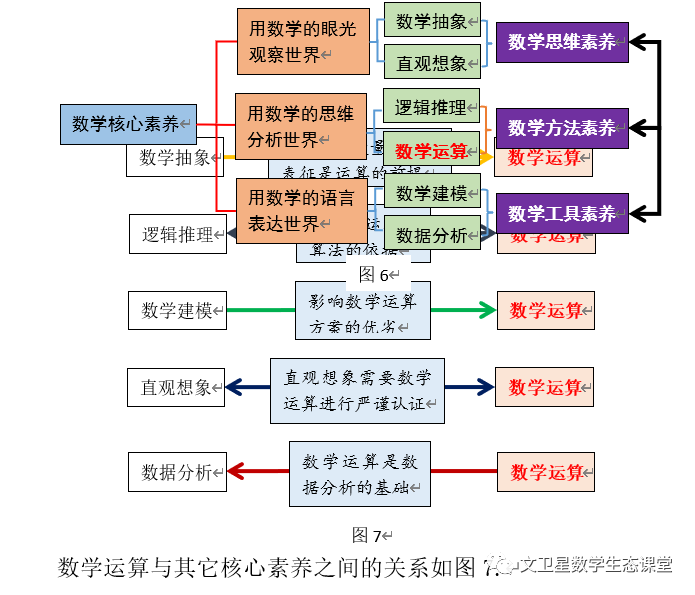
数学运算在核心素养中往往起到联结作用，因为它们彼此间的影响强弱不同，但总体上相互关联，所以在课堂教学中培养数学运算素养需要全面培养数学学科素养.

3.依据系统论原则培养学生数学运算

系统论认为系统是由相互作用和相互依赖的若干组成部分，结合成具有特定功能的有机整体.[5]一切事物、现象和过程均可看作有机整体，成为系统.在系统中，数学运算可以看作课堂教学的目标系统之一，也可以看作问题解决系统中一环.依据此理论，常见的解题流程图有循环结构（图8）与顺序结构（图9）.

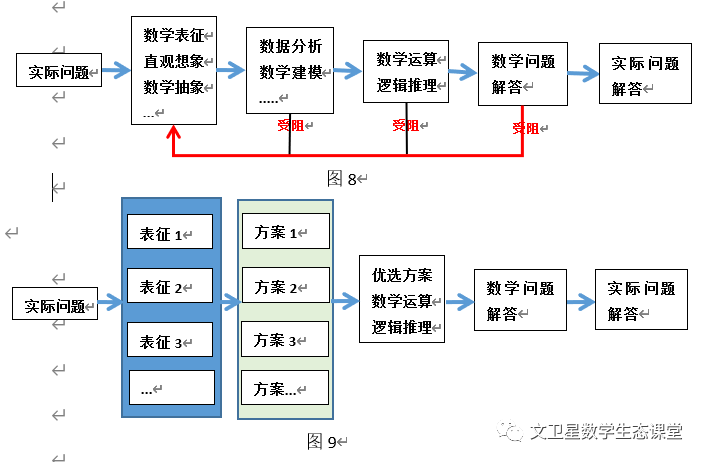
循环结构的特点是重复表征、建模、推理、运算等过程，每一次都是在预设顺利进行的情况下推进，当受阻时即重复解题过程.而顺序结构则是对实际问题进行多元表征，由表征结果进行多种方案预设，再优选方案，进行运算推理，得到数学问题解答，再回归实际问题结论.两种结构在解决问题时优劣与问题的难度有关，基于SOLO理论对数学问题进行分类，其中单点结构（U)与多点结构（M)选用循环结构较适用，而对于关联结构（R）与抽象扩展结构（E）则顺序结构效率更高.在数学教学中应让学生有意识地体验两种解题流程，感悟数学解题时核心素养在全流程的应用，特别是顺序结构中的表征活动与方案设计，应该作为教学的重点内容.

参考文献

[1]中华人民共和国教育部.普通高中数学课程标准2017版[M].北京：人民教育出版社，2018.1：7

[2]钟丽纯.基于SOLO分类理论的高考试题能力结构研究[J].地理教学，2018，12：43.

[3]中华人民共和国教育部.普通高中数学课程标准(实验)[M].北京：人民教育出版社，2013：11.

[4]中华人民共和国教育部.普通高中数学课程标准2017版[M].北京：人民教育出版社，2018.1：8

[5] 何克抗郑永柏 谢幼如.教学系统设计[M].北京：北京师范大学出版社，2002.10：5.

扫描ErWeiMa，gongzhong号“文卫星数学生态课堂”

往期推荐

文卫星：（视频）如何学习高中数学 第8讲 高一学生数学学习过程中心理调适

文卫星：（短视频）命题与充要条件

文卫星：（短视频）集合的包含关系与命题

文卫星：（短视频）如何学习高中数学公益讲座

文卫星：如何学习高中数学讲座 第7讲：如何写章末小结

文卫星：（视频）如何学习高中数学公益讲座 第6讲：如何预习

文卫星：（视频）如何学习高中数学讲座 第5讲：如何做数学作业

文卫星 ：（视频）如何学习高中数学公益讲座 第3、4讲：如何上数学课、如何记笔记

文卫星：（视频）如何学习高中数学 第二讲：初中骄子为何高中学习困难

文卫星：（视频）如何学习高中数学 第1讲：学习态度

文卫星：新教材必修1 每课讲与练 幂函数 （精讲篇）

文卫星：新教材必修1 每课讲与练 第13讲 函数的奇偶性 （答案）

文卫星：新教材必修1 每课讲与练 第13讲 函数的奇偶性 （训练篇）

文卫星：新教材必修1 每课讲与练 第13讲 函数的奇偶性 （训练篇）

文卫星：新教材必修 每课讲与练 第12讲 函数的单调性（精讲篇）

文卫星:新教材必修 每课讲与练 第12讲 函数的单调性（训练篇）

文卫星：新教材必修 每课讲与练 第12讲 函数的单调性（答案）

文卫星：新教材必修1 每课讲与练 第11讲 函数的概念 （精讲篇）

文卫星：新教材必修1 每课讲与练 任意角 （精讲篇）

文卫星：新教材必修1 每课讲与练 第角 （训练篇）

文卫星：新教材必修1 每课讲与练 第讲 任意角讲任意（答案）答案

文卫星：新教材必修1 每课讲与练 第10 讲 绝对值不等式（精讲篇）

文卫星：新教材必修1 每课讲与练 第10 讲 绝对值不等式（训练篇）

文卫星: 新教材必修1 每课讲与练 第10 讲 绝对值不等式（答案）答案

文卫星：新教材必修1 每课讲与练 第9讲 基本不等式 （精讲篇）

文卫星：新教材必修1 每课讲与练 第9讲 基本不等式 （训练篇）

文卫星：新教材必修1 每课讲与练 第9讲 基本不等式 （训练篇）答案

文卫星：新教材必修1 每课讲与练 第8讲 高次分式不等式（精讲篇）

文卫星：新教材必修1 每课讲与练 第8讲 分式不等式（训练篇）

文卫星：新教材必修1 每课讲与练 第8讲 分式不等式（答案）

文卫星：新教材必修1 每课讲与练 第7讲 解二次不等式 （精讲篇）

文卫星：新教材必修1 每课讲与练 第7讲 解二次不等式 （训练篇）

文卫星：新教材必修1 每课讲与练 第7讲 解二次不等式 （答案）答案

卫星文：新教必修1 材每课讲与练 第6讲 相等与不等 （精讲篇）

文卫星：新教材必修1 每课讲与练 第6讲 不等式的性质 （训练篇）

文卫星：新教材必修1 每课讲与练 第6讲 不等式的性质 （答案）

文卫星：新教材必修1 每课讲与练 第5讲 全称量词与存在量词（精讲篇）

文卫星：新教材必修1 每课讲与练 第5讲 全称量词与存在量词（训练篇）

文卫星：新教材必修1 每课讲与练 第5讲 全称量词与存在量词（答案）

文卫星：新教材必修1 每课讲与练 第4讲命题与充要条件（精讲篇）

文卫星：新教材必修1 每课讲与练 第4讲 充要条件（训练篇）

文卫星：新教材必修1 每课讲与练 第4讲 命题与充要条件（答案）

文卫星：新教材必修1 每课讲与练第3讲 集合的运算（精讲篇）

文卫星：新教材必修1 每课讲与练 第3讲 集合的运算（训练篇）A

文卫星：新教材必修1 每课讲与练 第3讲 集合的运算（训练篇）答案

文卫星：新教材必修1 每课讲与练 第2讲 集合的关系（精讲篇）

文卫星：新教材必修1 每课讲与练第2讲集合的关系（训练篇）

文卫星：新教材必修1 每课讲与练 第2讲 集合的关系（训练篇）答案

文卫星：新教材必修1 每课讲与练 第1讲 集合的概念（精讲篇）

文卫星：新教材必修1 每课讲与练 第1讲 集合的概念（精讲篇下）

文卫星：新教材必修1 每课讲与练 第1讲 集合的概念练习A、B组

文卫星：必修1 第1讲 集合的概念（训练篇）C组+A组答案

文卫星：必修1 第1讲 集合的概念（训练篇）B、C组答案

俞廉洁 杨元韡：以“异面直线所成角”的教学设计谈立体几何的概念教学

朱宸才：解法对比探究竟 变式拓展出新意 ——以阿波罗尼斯圆为背景的一类中考最值问题探究

文卫星：爱 学 生 的 艺 术

李晶 李德安 孙雪梅：中学“三段式”自主学习法

文卫星：减负，数学老师可做些什么

陆 建：基于多元表征，完善CPFS结构 ——以“椭圆”概念教学为例

高峥：数学概念理解差错的分析流程之差错分析与诊断*

文卫星：新高一如何适应高中数学学习

杨元韡 耿晓华:对解题教学中数学直觉的价值及培养途径的思考

周学玲 谢贝贝：生态课堂中初高中数学自然衔接 ——人教新教材基本不等式实验教学

文卫星：如何把“数学生态课堂”理念落实在实践中

吴世星 陈广前：正多边形内定线段滑动的中点轨迹探究

张启锋：基于“一个主题、三条主线”的数学教学设计与实践

徐 辉:让课堂因学生提出问题而精彩 ——以一节解析几何复习课为例

张建国， 肖恩利：新课标下沪编教材“三角不等式”的教学设计

张乐瑛:类比过程，提升数学能力

翁昌来 孙雯 谢敏 王瑛：重构单元知识框架，提升逻辑推理能力 ——以坐标平面上的直线章节复习课为例

翟洪亮 蔡旭林：注重方法类比 培养理性思维

孙 鋆、唐恒钧：基于问题链的数学法则教学设计与实践

李响 黄继红：“单元统整”背景下序言课教学设计的思考与实践

唐恒钧 张维忠 数学问题链教学：缘起、进展与展望

冯一成：一次测试结果引发的教学思考

渠东剑 ：“八省联考”数学卷分析及启示

戚有建:一道解几定值题引起的研究

黄桂君:解析几何复习教学重在运算淡化思路

钟国平：多视角灵活切入多变量最值问题

蒋建华：数学老师的“牛年情思”

殷玉波：素养导向下高三数学复习单元设计案例分析 ——以圆锥曲线中的定点问题为例

丁明忠：立足核心素养命好题

唐永：开展补偿式教学，提高高三一轮备考效率

朱卫萍：思维显身手，方法现本质——一道解三角形题的探究

党忠良：创造性的教才能创造性的学——椭圆及其标准方程教学实践与反思

姚必魏、李林静：巧妙构造辅助函数 探究零点范围问题

高宇：在公式教学中落实逻辑推理素养——以“两角差的余弦公式”为例

张立：研究课本素材，引导高三复习

周芸：教材习题的教学策略与实践

孟泰：数学抽象的两层次与两面性

李忠贵、郭建华：“自组织”理论下的数学解题教学的实践与思考 ——以一道高三模拟考试题为例

马晴燕：教师多元角色担当 促进学生素养发展“自组织”理论下的数学解题教学的实践与思考 ——以一道高三模拟考试题为例

杨敬民：2021年高考甲卷立体几何题的纯几何解法

张晓斌：从定义出发，体现数学思想与方法的探究课 ――对课例《球的表面积和体积》的点评

梅颖颖：全国优秀课例----“球的体积和表面积”教学设计

曾月波：2021年普通高等学校招生全国统一考试理科数学甲卷第21题解答

文卫星、张润平：2021年新高考Ⅰ卷第21题“秒杀”解法及16题解答

---

[1]基金项目：江苏省教育科学“十三五”规划重点课题“高中生数学批判质疑能力的实践研究（B-b/2018/02/56）”.