【初中数学】辅助线6种典型问题!逢考必有!

发布于 2021-09-13 20:13 ，所属分类：中考数学学习资料大全

初三数学•上册内容

要知道明年你们将迎来人生中的第一次选拔性考试——中考，所以，这一年的时间都是很宝贵了。不想落后他人，抓紧预习起来。今天，和大家分享的是初三数学【辅助线系列】6种典型问题抓紧掌握，逢考必有，丢分可惜！


01

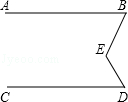
如图，∠E＝∠B+∠D，猜想AB与CD有怎样的位置关系，并说明理由．


【分析】延长BE交CD于F，通过三角形外角的性质可证明∠B＝∠EFD，则能证明AB∥CD．
【解答】解：延长BE交CD于F．
∵∠BED＝∠B+∠D，
∠BED＝∠EFD+∠D，
∴∠B＝∠EFD，
∴AB∥CD．
解法二：如图，过点E作∠BEF＝∠B（EF在∠BED内），
所以AB∥EF（内错角相等，两直线平行），
因为∠BED＝∠BEF+∠FED＝∠B+∠D（已知），∠BEF＝∠B（已作），
所以∠FED＝∠D，所以CD∥EF（内错角相等，两直线平行）
所以AB∥CD（如果两条直线都和第三条直线平行，那么这两条直线平行）．
02

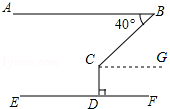
（2016•十堰）如图，AB∥EF，CD⊥EF于点D，若∠ABC＝40°，则∠BCD＝（　　）

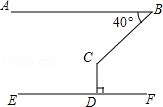
A．140°B．130°C．120°D．110°


【分析】直接利用平行线的性质得出∠B＝∠BCG，∠GCD＝90°，进而得出答案．
【解答】解：过点C作CG∥AB，
由题意可得：AB∥EF∥CG，
故∠B＝∠BCG，∠GCD＝90°，
则∠BCD＝40°+90°＝130°．
故选：B．

03

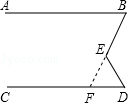
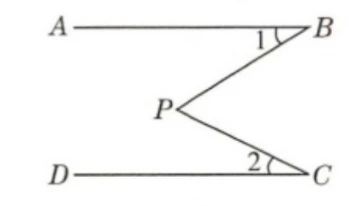
如图，AB∥CD，P为AB，CD之间的一点，已知∠2＝28°，∠BPC＝58°，求∠1的度数。


【解答】解：过点P作射线PN∥AB，如图1所示
因为PN∥AB，AB∥CD，所以PN∥CD
所以∠4＝∠2＝28°
因为PN∥AB，所以∠3＝∠1
因为∠3＝∠BPC－∠4＝58°－28°＝30°
所以∠1＝30°

04

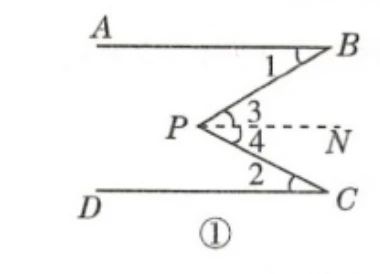
（1）如图1，若AB∥DE，∠B＝135°，∠D＝145°，求∠BCD的度数.

（2）如图1，在AB∥DE的条件下，你能得出∠B、∠BCD、∠D之间的数量关系吗？并说明理由．

（3）如图2，AB∥EF，根据（2）中的猜想，直接写出∠B＋∠C＋∠D＋∠E的度数


【解答】解：（1）如图，过C点作CF∥AB，所以∠B＋∠BCF＝180°
因为AB∥DE，所以CF∥DE
所以∠FCD＋∠D＝180°
所以∠B＋∠BCF＋∠FCD＋∠D＝180°＋180°
即∠B＋∠BCD＋∠D＝360°
所以∠BCD＝360°－∠B－∠D＝360°－135°－145°＝80°
（2）∠B＋∠BCD＋∠D＝360°，
理由：如图，因为CF∥AB
又因为AB∥DE，所以CF∥DE
所以∠B＋∠BCF＝180°
所以∠B＋∠BCF＋∠FCD＋∠D＝180°＋180°
即∠B＋∠BCD＋∠D＝360°
（3）∠B＋∠C＋∠D＋∠E＝540°

05

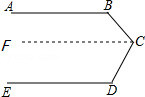
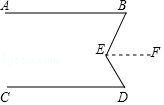
如图，∠BEC＝95°，∠ABE＝120°，∠DCE＝35°，则AB与CD平行吗？请说明理由．


【分析】过点E作EF∥AB，根据∠ABE＝125°可求出∠BEF的度数，进而得出∠FEC的度数，由此可得出EF∥CD，故可得出结论．

【解答】解：AB∥CD．
理由：过点E作EF∥CD，
所以∠FEC＝∠DCE＝35°．
因为∠BEC＝95°
所以∠BEF＝95°－35°＝60°
又因为∠ABE＝120°
所以∠ABE＋∠BEF＝180°
所以AB∥EF
又因为EF∥CD，所以AB∥CD．
06

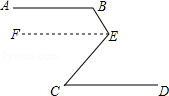
如图，AB∥CD，BE平分∠ABF，DE平分∠CDF，∠BFD＝120°，求∠BED．


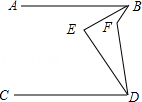
【分析】连接BD，过F作FG∥AB，由AB∥CD，得到FG∥CD，利用两直线平行内错角相等，得到两对角相等，进而求出∠ABF+∠CDF的度数，由BE平分∠ABF，DE平分∠CDF，利用角平分线定义得到∠EBF+∠EFF的度数，在三角形BFD中，利用内角和定理得到∠FBD+∠FDB的度数，进而求出∠EBD+∠EDB的度数，求出∠BED度数即可．

【解答】解：连接BD，过F作FG∥AB，由AB∥CD，得到FG∥CD，
∴∠ABF＝∠BFG，∠CDF＝∠DFG，
∴∠BFD＝∠ABF+∠CDF＝120°，∠FBD+∠FDB＝60°，
∵BE平分∠ABF，DE平分∠CDF，
∴∠EBF+∠EDF＝（∠ABF+∠CDF）＝60°，
∴∠EBD+∠EDB＝∠EBF+∠EDF+∠FBD+∠FDB＝120°，
则∠BED＝60°．





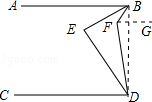
孩子为什么要上一个好高中？这是我听过最好的答案！

家有青春期孩子，父母时刻谨记“三颗心”！很重要！

初三下学期怎么学？考前4个月如何复习？

编辑：冬冬老师

更多内容请gongzhong号平台：初中乐学 ID：cslx226

声明：文章来源于网络，版权归原作者所有，如有侵权联系小编立即删除！

点亮“在看”，您的支持是我不断努力的动力

相关资源