数学微论文

五年级孩子平常写作文的字数大概要求在500字以内，而数学小论文要写清楚，至少要千把字吧。单单看字数，有些孩子就怕了。好吧，那就从数学微论文开始慢慢写。继上周发布的之后，我们再来看几位小仙女的作品。

方格纸中的数学

五（1）蔡以轩

一、问题提出

在做几何图形的题目里，看到了这样的一个题目:

图中相隔的小正方形最小正方形的面积3平方厘米，这个多边图形的面积是多少平方厘米 。

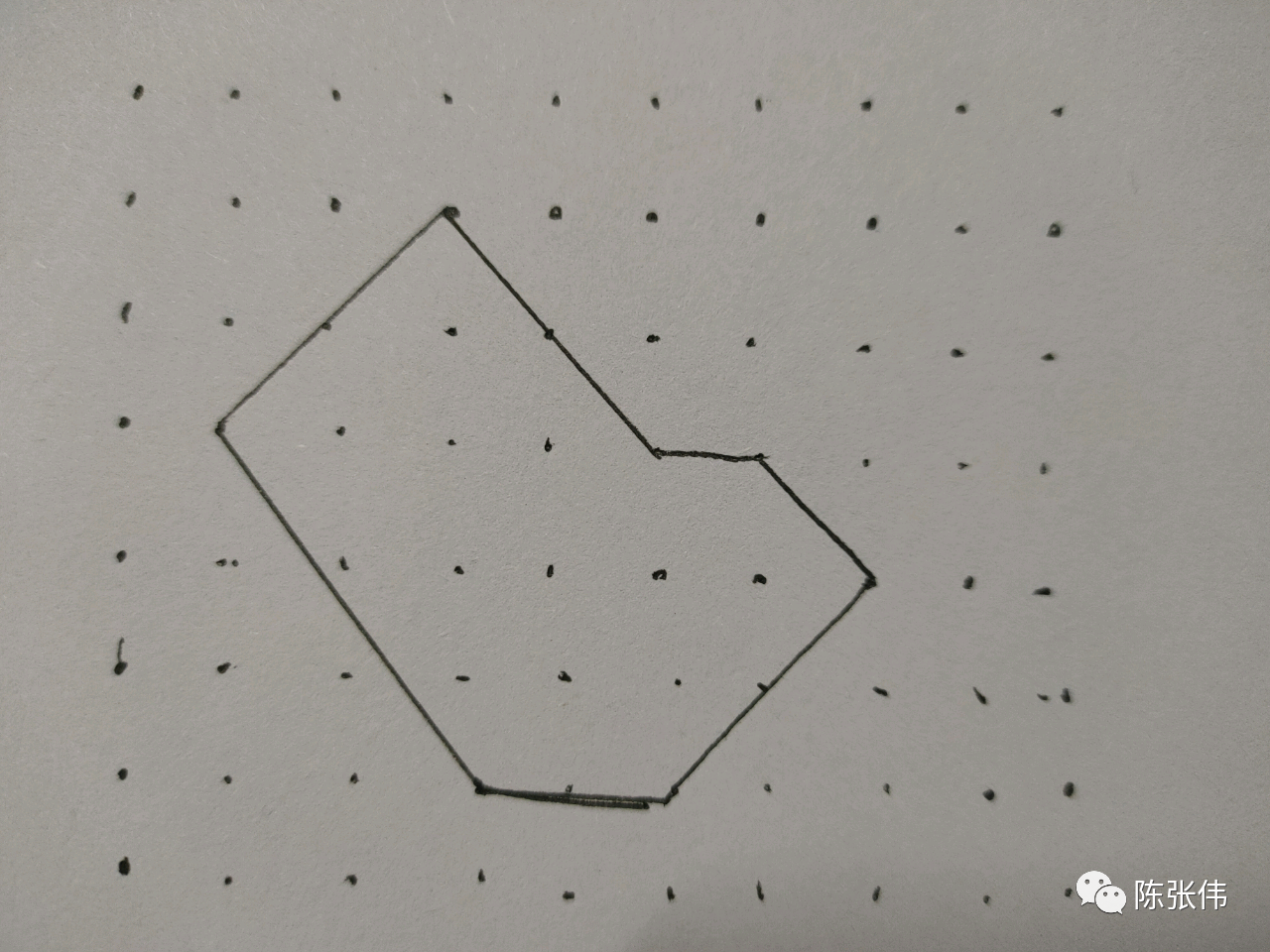
咦？这是什么图形，还有七条边，七个角，而且还要求它的面积，可不容易，里外还有很多小点，到底该怎么求呢？

二、研究过程

几何的起源在古埃及人聚居在尼罗河附近，以在河边的农田耕作为生，可是尼罗河每隔一段时间河水会泛滥，河水泉涌上岸，把河边的农田淹没，冲毁农田的边界，所以，每次河水泛滥后，埃及人都要重新划分农田的范围和界限。埃及人在划分土地时，发现很多不同形状的农田都可以分割为几块较细小的三角形农田例如:

1块长方形农田、两块大小相同的三角形农田、一块梯形农田、三块大小相同的三角农田。这些不同形状白勺农田，就是我们认识的不同几何图形，把农田分割成几小块农田，就是几何图形的分割，几何图形的分割和添补，根据一些基本图形，也是规则图形，如:平行四边形、正方形、梯形，然后根据这些图形的面积公式，加起来或减去，平行四边形的面积公式 :底×高，正方形的面积公式 :边长×边长，梯形的面积公式:（上底+下底 )×高÷2。

其中就有一些不规则图形，如同上面的一道题目。正方形、长方形、三角形都是规则图形，而有些图形有很多边、角，这就是不规则图形，如果要求它们的面积，就只能把它们分割或添补，上面这个不规则图形，就可以使用分割法，把它分割成一个三角形和一个正方形，再按照三角形和正方形的面积公式，求出整个不规则图形的面积。

我发现了当中间格点数不变，边点点数扩大，图形面积也会扩大，如果边点点数不变，图形面积是随着中间格点的扩大或缩小，正方形格点图形面积公式，（内点+边点÷2-1）ⅹ单位正方形面积，这个公式名叫皮克定理，每个高点图形都可以根据皮克定理来写。接下来我们就可以解决这道问题，（12+11÷2-1）×3＝49.5。

那如果把题目改一下呢？图中相隔的小三角形的三角形面积是2平方厘米，这个多边形图形面积是多少平方厘米？

该怎么办呢？皮克定理只能算小正方形的面积，可是不能算小三角形的面积呀！这时我发现了两个三角形， 刚好拼凑成一个正方形，有了！每两个三角形就能组成一个长方形，那么原本一个长方形的面积是3平方米，三角形以后，算两个才是三平方厘米，那么我们就可以从皮克定理再乘以二 ，就求出最小面积是三角形的方格问题了。

三、总结

割分和添补，会把不规则图形，分割或添补规则图形，解决不规则图形正方形的问题，可以运用皮克定理（内点+边点÷2-1 ）×单位正方形面积，如果是解决不规则图形三角形的问题，可以在皮克定理后面乘2 ＝（内点+边点÷2-1 ）×单位三角形的面积×2。

数学不仅是在书上，更在生活中，就如埃及人分割农田一样 。

什么是“数字黑洞”

五（1）许安辰

今天的数学课上，我们学的内容是关于“数字黑洞”认识。陈老师跟我们详细讲了“数字黑洞”。这是一个新的知识内容，我觉得很有趣。

数字黑洞是指自然数经过某种数字运算之后陷入了一种循环的境况。例如，选四个不同的数字，按从大到小的顺序排成一个数，再按从小到大的顺序排成另一个数，用大的数减去小的数（如1、2、3、0，就可以用3210-123），用所得的四位数重复上述过程，最多七步6174。即7641-1467=6174。

老师让我们试了试，果然，我写的“1、2、3、4”这组数字验证了老师说法,是“4321-1234=3087,8730-378=8352,8352-2358=6174”这样计算的。林士强同学说自己写了十几个算式，还是没有得到6174这个数字。老师让他再仔细算算，看看是不是哪儿算错了。林士强特意用计算器来验算，结果发现真的是自己算错了。

这件小事过后，我又算了“3、4、5、6”这组数字，过程是这样的，如下所示“6543-3456=3087,3087-378=8352,8352-2358=6174”三步就算出来了。紧接着，我又写了四个奇数“1357”，即“7531-1357=6174”，我很疑惑怎么只用一步就得到6174这个数字啊？我立马用“8、2、4、6”这组数字来算，即8642-2468=6174,也是算一步就有结果了。这真是一个惊喜的发现！我心里很激动，哈哈哈。

班上的敖宇韩和林士强一起发现了另一个“惊天大秘密”！这个秘密是这样的，“1、2、3、4”，“2、3、4、5”，“3、4、5、6”，“4、5、6、7”，“5、6、7、8”“6、7、8、9”这样连续的自然数，用最大的数减去最小的数，它们第一步算出来的结果是“3087”，真是太神奇了。

“数字黑洞”的知识太有趣，数学的知识海洋真是奥妙无比，只要认真去听课，认真去思考，都会有不同的收获。

由数字黑洞引发的思考

五（2）林晨茜

一天我从数学书上知道了数字黑洞，也初步了解了数字黑洞，我知道了数字黑洞又称黑洞数又称陷阱数，类具有奇特转换特性整数，任何数字不全相同的整数，经有限重排求差操作，总会得到某些数，这些数即黑洞数重排求差操作即把组成该数字重排得大数减去重排得小数，就是指自然数经过某种数学运算之后陷入了一种循环的境况。

例如，任选四个不同的数字按从大到小的顺序，按从小到大的顺序，排成一个数，用大数减去小数，如(1，2，3，0，就用3210减123)用所得结果的四位数重复上述过程最多七步必得6174 7641-1467=6174仿佛掉进了黑洞，永远出不来。可我认为这只是巧合，所以一心想去试一试，就写了三个式子。

(1)2，7，6，8 (2)6，7，8，9

8762-2678=6084 9876-6789=3087

8640-468=8172 8730-378=8352

8721-1278=7443 8532-2358=6174

7443-3447=3996 7641-1467=6174

9963-3699=6264

6642-2466＝4176

7641-1467=6174 (3)7，4，5，6

7641-1467=6174 7654-4567=3087

8730-378=8352

8532-2358=6174

7641-1467=6174

当我写完第一个式子的时候只觉得是一个巧合，因为我算到6174已经用了七步，但答案确实是6174，所以我又算了第二个式子，算完第二个式子的时候我吃惊不已，因为这次我只用了三步就求出了6174。可我还是有点不相信，数字会死循环，所以又算了第三个式子。第三个式子我也用了三步就求出了6174这更让我吃惊了。这下我不得不相信数字会死循环，数字黑洞真神奇。