径向基函数的SPSS操作
发布于 2021-04-26 05:02 ,所属分类:知识学习综合资讯

作者:王鹏审稿:柏安之封面:吉江


本文主要介绍径向基函数在SPSS中的操作应用,并且介绍了径向基函数与多层感知器在SPSS中操作的异同之处。
由于径向基函数在操作界面和输出结果方面和多层感知器非常类似,因此,这里仍然采用低体重出生儿的样本数据,即neural-network.sav文件进行分析。
1.操作步骤如下:
(1)选择“分析”→“神经网络”→“径向基函数”选项;
(2)和多层感知器操作相同,将变量“low”选入“因变量”,将变量“ht”选入“因子”,将“lwt”和“pt”选入“协变量”。
(3)点击“确定”按钮。
在两者的操作界面中,除了“体系结构”选项不同之外,其余选项卡的内容完全相同。两者的“体系结构”界面如图1所示。多层感知器的“体系结构”选项用来指定神经网络结构,一般软件程序会自动选择最好的结构,不需要手动修改。径向基函数中“体系结构”是用来建立一个隐藏的径向基函数层。两个神经网络模型中“体系结构”的各参数,绝大多数时候采用自动搜索确定最佳的单位数和最佳允许重叠数量即可,因此很多时候也不需要修改。当然,如果在做神经网络分析时,特别强调需要修改隐含层或者输出层激活函数类型时,才会手动修改。

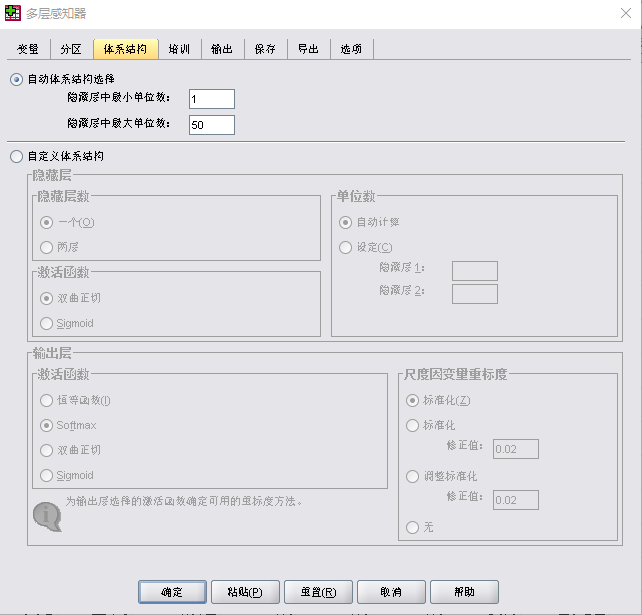
图1
2.结果分析
| 表1 案例处理汇总 | |||
| N | 百分比 | ||
| 样本 | 训练 | 139 | 73.5% |
| 测试 | 50 | 26.5% | |
| 有效 | 189 | 100.0% | |
| 已排除 | 0 | ||
| 总计 | 189 | ||
| 表2 网络信息 | |||
| 输入层 | 因子 | 1 | 是否患有高血压 |
| 协变量 | 1 | 产妇体重 | |
| 2 | 本次妊娠前早产次数 | ||
| 单位数 | 4 | ||
| 协变量的重标度方法 | 标准化 | ||
| 隐藏层 | 单位数 | 2a | |
| 激活函数 | Softmax | ||
| 输出层 | 因变量 | 1 | 低出生体重儿 |
| 单位数 | 2 | ||
| 激活函数 | 恒等 | ||
| 错误函数 | 平方和 | ||
| a. 由检验数据标准确定:隐藏单位的"最佳"数量为检验数据中产生最小错误的单位。 | |||
表1和表2说明有139个样本数据用于训练,其余的50个样本用于测试,所生成的模型有一个隐藏层(隐含层),其中包括两个神经元,通过与上节的多层感知器模型相比较,发现无论何种神经网络算法,最终的判断结果都是单隐藏层有两个神经元且可以完全容纳所有的样本数据信息。
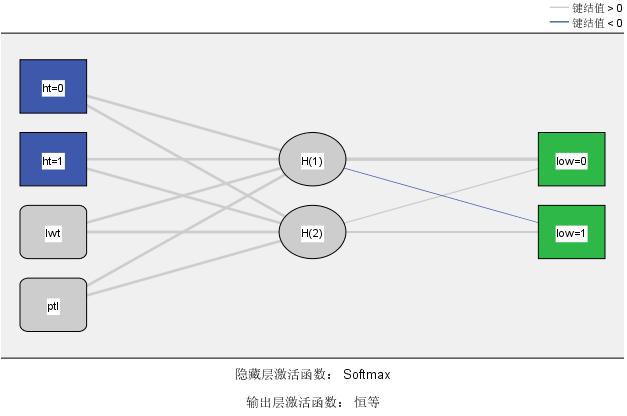
图2
图2为所建立的径向基网络的结构示意图,可见网络基本结构框架和多层感知器的结构图相类似。分类变量被拆分成多个哑变量节点,从而被容纳在网络结构中,但由于在SPSS径向基模型操作中使用的是默认的标准化径向基函数(见图1),因此,结构中没有出现常数项(截距)节点。
| 表3 模型汇总 | ||
| 训练 | 平方和错误 | 28.205 |
| 百分比错误预测 | 31.7% | |
| 培训时间 | 0:00:00.130 | |
| 测试 | 平方和错误 | 9.412a |
| 百分比错误预测 | 28.0% | |
| 因变量: 低出生体重儿 | ||
| a. 隐藏单位的数量由检验数据标准确定:隐藏单位的"最佳"数量为检验数据中产生最小错误的单位。 | ||
从表3可看出,模型对样本数据的整体预测错误率在25%到35%之间,通过比较上一节多层感知器的分析结果,发现径向基函数模型比其要高3%到4%。
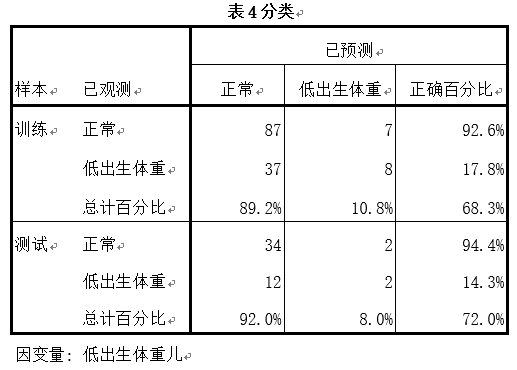
从表4可以发现,样本训练集中低出生体重儿的预测正确率为17.8%,测试集的预测正确率为14.3%,也比多层感知器模型的预测准确率要低。因此,从这两种模型分析来看,该样本数据更适合用多层感知器神经网络模型分析。

gongzhong号,回复20190517即可获得数据~














![[强基计划]刘雯高二数学寒假直播班6讲2021寒](https://static.kouhao8.com/cunchu/cunchu7/2023-10-08/UpFile/defaultuploadfile/2023051202/909-1.jpg?x-oss-process=image/format,webp/resize,w_88/crop,w_88,h_88,g_nw)










![[Java框架] 尚硅谷Shiro框架视频基教程](https://static.kouhao8.com/sucaidashi/xkbb/f144ec034b28940f9c43816c6310eb32.png?x-oss-process=image/format,webp/resize,w_88/crop,w_88,h_88,g_nw)
![【蒋德赛物理】高三物理强基计划视频课程(2022暑假)[百度网盘下载]](https://static.kouhao8.com/cunchu/cunchu7/2023-05-18/UpFile/defaultuploadfile/230430ml/232-1.jpg?x-oss-process=image/format,webp/resize,w_88/crop,w_88,h_88,g_nw)





相关资源