中考数学之求函数表达式与点的坐标

纵观广东省近几年的中考数学试卷，在最后5道题中，几乎每年都会考到一类题型：函数综合题，所考查的一般为一次函数+反比例函数，或者二次函数+一次函数的组合，其中还会囊括一些其他方面的知识点，比如：三角形、四边形、不等式（广州卷二次函数压轴题似乎不满足这个套路，2021年广东省卷25题非常像往年广东省卷与往年广州卷杂交的产物，还是部分满足以上规则，故仅有广州卷二次函数压轴题不在讨论之列）。

此类题比较灵活，难度中等偏上，有的时候还会以压轴题出现（二次函数综合）。题目一般设置2~3问，前面一般会要求我们求解出题目中出现的函数的解析式或点的坐标，看似复杂，其实可以说是压轴题中的福利部分。对于基础好的同学，这些分值可以比较轻松拿到，但是有部分同学苦于要处理的信息太多，或者因为摸不清套路，会很可惜的与这几分失之交臂。

出于想帮助更多同学把这明明可以很容易拿到的分尽量拿到的目的（会做的同学可以不用往下看了，对你可能帮助不大），我将把解决这类问题的方法在此做一个简单又不失深度的说明。

首先，让我们来看看这类题目和问题都长什么样：

其中会给出若干函数图像以及表达式，还有图像上一些点的信息，这些表达式和点的信息中一定会有未知的参数。所以，解决这类问题（求函数解析式或点的坐标）一个很重要的思考方向就是——列方程：

求未知点的坐标，靠已知函数的表达式去列方程；

求未知函数的表达式，将已知点的坐标代入去列方程。

因此，我们需要从题目中找寻的东西无外乎两样：

函数的表达式；

函数图像上的点以及点的横、纵坐标。

下面是具体思路：

（1）从题干中查找函数和点的信息。

在找的时候请注意观察函数的图像，图像的形状以及相关线段的长度，直线与直线之间的角度，都可以给我们带来很多信息。

例如：假设

的图像如下：

我们能轻易的得从这几条结论——

这些信息可能与我们求解函数解析式或点的坐标没有直接关系，但是可以用于粗略的验证我们的结果（如果最后算出来b < 0，和函数图像形状有悖，说明算错了）。

从题目中有目的地去找寻以上两样信息是十分容易的事情，大部分情况下，函数表达式和点的数据都是直接给出的。

当然，出题人也可能有意将部分数据隐藏于一些其他的条件，比如：线段的长度关系，几何图形的面积，中点，直线与直线夹角的度数，甚至是不等式…等条件当中。

若是如此，我们需认真思考这些元素与点的横、纵坐标或是函数表达式的参数之间存在何种联系，并将其进行翻译。

例如：直线L: y = kx + b与x 轴之间夹角为45°，这条信息实则在告诉我们：k = 1 或 -1.

（2）按以上要求整理信息之后，直接列方程——

将已知点的坐标代入未知的函数表达式中，可以列出关于函数表达式未知参数的方程；

将已知的函数表达式进行联立，可以得到关于交点坐标的方程。

下面我们按照这种思路来解决2020年广东省卷的一道二次函数综合题的1、2问：

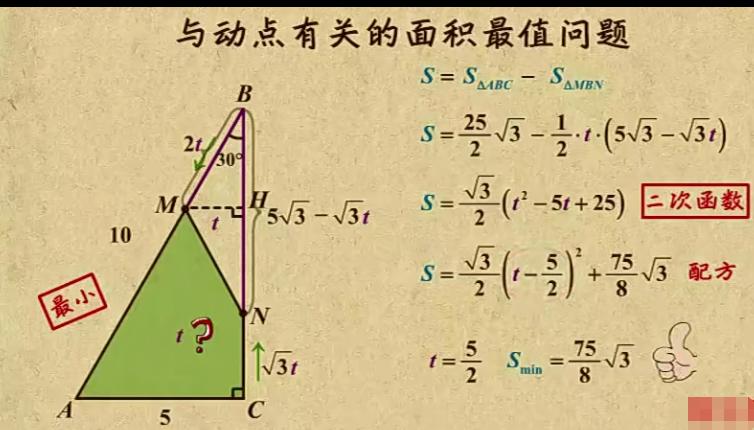
具体分析和步骤如下——

至此，该题前两问解答完毕。其中并未有什么十分精妙的步骤，都是有套路可循。如果非要找题目中的难点，那便是如何准确的将几何条件转化为：与坐标或者函数解析式有关的条件这一步上。要熟练的做到这点，只能通过一定的专项练习去熟悉这种思路了。

其实今年的广东省卷二次函数压轴题也是可以通过这种套路去思考和解决的，很多同学做不出来，我个人觉得是因为广东省卷往年在不等式这块实在考的比较浅，导致很多同学疏于这方面的练习。后续我会对这道题专门作一篇讲解。

另外，由于本人对gongzhong号平台使用方法的生疏，导致排版等各个方面显得乱七八糟，也不知道如何插入各种数学表达式，很苦恼。我将尽快找出解决方法，请大家谅解，文中如有事实错误，也请指出，感谢！