2021广东中考数学特评(三)

上期我们讲解了2021广东省中考数学选择题部分，同时透过这部分内容在初中阶段与高中阶段知识点的联系，感知到广东省未来对于初中阶段可能存在的教育改革方向。续上期，本期将为各位家长与同学讲解的是选择题部分，看看是否能与选择题部分有相同的预期效果。

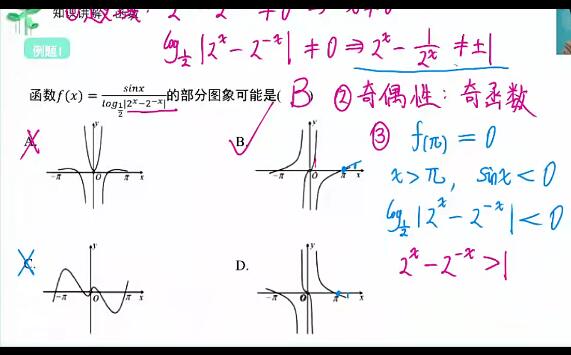
第15题对于基础扎实的同学而已思路上并不难想到，因为所求式子是仅含x一个未知数的等式，所以可以围绕着求解出x作为全题的目标，进而将x+1/x=13/6转化为x²-13/6x+1=0，进而题目变作求解一元二次方程的问题，最后求解出x值后，带入题目所求的x²-1/x²之中即可求得答案，另外也可以利用平方差公式将目标式子转化为（x+1/x）（x-1/x）的形式求解。综合来看，本题思路上并不算难，题目不算新颖，但计算量较大，对于同学们运算要求较高，另外，因为解二次方程对配方法与公式法的考察，建议同学们在课余时间多熟记一些平方数，以增强个人对于数据开方的敏感度，减少运算量，对于初高中阶段学习都会大有裨益。本题求解过程如下。

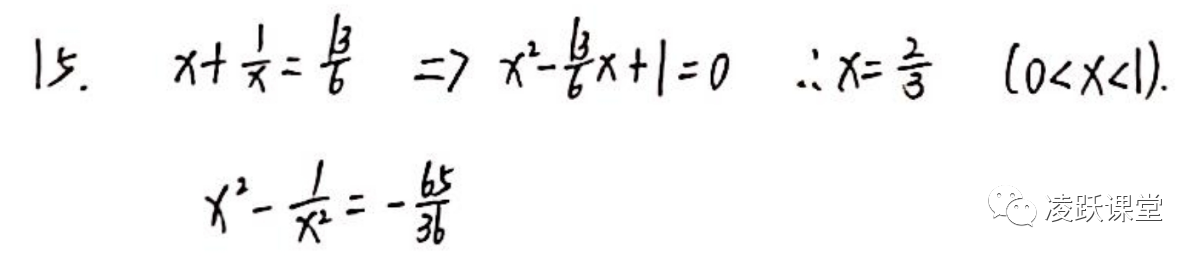
第16题不同于第15题，第15题纯粹是代数与运算量方面的问题，而第16题则是思路层面的找寻与探索。对于平行四边形的特性了解，以及对于三角函数的认知等等。因为需求的是sin∠BCE，那么对于初中阶段而言，首先需要明确的是所求∠BCE落在哪个直角三角形中，若没有现成的直角三角形，则需要进行构造，显然此处即是需要考虑如何构造包含∠BCE的直角三角形，根据已有条件与图形不难考虑到作BH⊥CE，那么问题就转化成了求解BH与BC上，至此，话分两头，一是求解BC，一是求解BH。

1. BC：显然BC作为平行四边形的边，是较容易求解的部分，所以优先求解BC，由平行四边形特性知，BC=AD=5。

2. BH：BH的求解即是本题的难点所在。显然CH的求解也缺乏条件，因此依靠CH求解BH的思路断了，须得另觅他法。既然在△BCH中无法解决，那么就需要将视野逐步放大，以扩充条件，此时看到△BCE中，

   BE=AB-AE=9,

   CE=√CD²+DE²=4√10，

   BC=5，

   条件得到这里，再求解sin∠BCE，很多高中的同学就要说了，这不就是高中的余弦定理了嘛。没错，本题从某方面而言，确实是对高中阶段余弦定理的考察，但对于初中阶段的同学们尚未学习余弦定理只得另辟蹊径。考虑到BH是△BCE中BE边上的高，而CE，BE，及CE边上的高CF=ED皆为已知量，由此可以利用等面积法，求解出BH的值。

3. 最终由BH/BC求出sin∠BCH=sin∠BCE.参考求解过程如下。

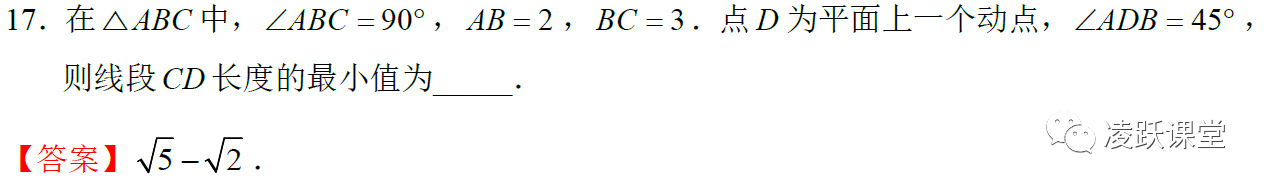
第17题是广东省中考在2020年改革做的题目类型修订，作为额外补充的一道填空压轴题，难度本就不容小觑。去年是围绕着轨迹与动点展开考察，而今年也自然离不开这个影子，这是情理之中的，但意料之外的是，它开拓性的将动点问题从线的问题扩充到了面上，使得同学们更难考虑到动点的位置，算是将动点问题难度又提升了一个档次。

层次较好的同学能够按照题目所给条件绘出右图已属不易，右图向左图的转化就需要同学们对于初中知识有非常深刻的理解了。接下来将一步步分析给同学们看，如何解决这类问题：

1. 点D是平面上一个动点本身是一个很棘手的问题，不同于以往的动点处于某直线上，此时的动点显得更加灵活和琢磨不定，很多同学也因此无法作图。但所有动点问题解决办法都可以归结为“以静制动”四个字，即通过相关定点去限制动点的运动。注意到此处∠ADB=45°，AB是定直线，此时需要同学们对于圆的知识有很深刻的理解了。定直线AB所对的∠ADB=45°恒成立，其实就是圆当中的定弦AB所对的圆周角恒为定值（同一段弧或弦所对的圆周角相等），因此可知D点处于以AB为弦的圆的轨迹上。但因为圆的图像确定是需要圆心位置 与直径的，因为我们依旧无法作出图2，有些同学可能觉得到这里思路又断了，但别急，注意考虑到∠ADB的实际数值——45°，在知道题目又转换到圆的问题时，应当大胆考虑到圆的其他定理，脑海关键词搜索不难发现，同弦（弧）所对的圆周角等于圆心角的一半，因此 ∠AOB=90°，而A，B，D作为圆O上的三点，于是有半径r=OA=OB=OD，在等腰Rt△AOB中，AB=2，所以r=AO=BO=DO=√2。即点D在以O为圆心，以r=√2为半径的圆上。

   至此我们已经全程按照同学们能够理解的逻辑去一步步引导同学们了解如何解决本题作图问题了。

2. 如果能够作出上图，说明同学们的思维强度 已经到达了一定的程度，接下来回顾到题目目标所求的CD最小值问题，对大家来说即是信手拈来之事。何时CD有最小值呢，无论从△OCD两边之和大于第三边出发还是三点共线值最小出发结合图像都可以发现，当D处于OC边上，即O，D，C三点共线时，CD有最小值，于是将问题转化为对OC长度的求解上即可求解出最终答案。具体求解步骤如下。
   

2021广东中考数学填空题整体难度偏大，主要难度集中在16,17题，第16题衔接对标高中余弦定理，第17题则是对考生思维强度及初中知识理解要求很高，甚至也给一些长期居于一线但习惯广东省中考简单模式的老师们当头一棒。与选择题部分同样的，填空题部分对于未来的中考走向或许也指向了高中知识的对标与初中知识点的深度理解上了。接下来几届的考生应当打破题海战术旧思维，将自己超脱出课本题型的禁锢中，从本质上去理解数学的几何与代数魅力，当然对于农村及偏远地区教育应激性是很有限且缓慢的，家长同学们一定要多了解发达地区教育强省的一些教学与考察，将自身的眼界开拓，才有可能在这场教育大内卷中成为幸存者。如有疑问，欢迎联系下方工作室！如有帮助，感恩转发，在看，点赞，一键三连！