中考数学阅读理解解题策略

1 问题呈现

题目《道德经》中的“道生一，一生二，二生三，三生万物”道出了自然数的特征．在数的学习过程中，我们会对其中一些具有某种特性的数进行研究，如学习自然数时，我们研究了奇数、偶数、质数、合数等．现在我们来研究另一种特珠的自然数——“纯数”．

定义：对于自然数n，在计算n+(n+1)+(n+2)时，各数位都不产生进位，则称这个自然数n为“纯数”．例如：32是”纯数”，因为计算32+33+34时，各数位都不产生进位;23不是“纯数”，因为计算23+24+25时，个位产生了进位．

(1)判断2019和2020是否是“纯数”？请说明理由；

(2)求出不大于100的“纯数”的个数．

2 试题分析

此题以中国哲学著作《道德经》展开，揭示了自然数的基本特征：即表示物体个数的数，充分考查了学生的数学文化素养.其主要考查内容为数与式，让学生根据所给的新定义，进行模仿与创造，特别是多次渗透分类讨论思想，要求学生不仅具有扎实的数学基础，还要有严谨的思维能力，因此这道题看似简单、得分容易，但是要得满分却实属不易.

3 解法赏析

3.1 对第(1)问的探究

该问题只需要依次对2019、2020进行分析，正确解答过程如下：

2019不是“纯数”，2020是“纯数”.理由如下：

由于在计算2019+2020+2021时，个位计算时是9+0+1=10，所以计算过程中产生了进位，因此推断2019不是“纯数”.

而在计算2020+2021+2022时，个位0+1+2=3，十位2+2+2=6，百位0+0+0=0，千位2+2+2=6，各数位的计算过程中都没有产生进位，因此推断2020是“纯数”.

3.2 对第(2)问的探究

解法一根据纯数的位数进行分类讨论

由题意得，当“纯数”n为一位数时n+(n+1)+(n+2)=3n+3<10，所以可以判断n=0，1，2，即在一位数的自然数中，“纯数”有3个.而当“纯数”n为两位数时，需满足的条件为：个位不超过2，十位不超过3时，才能符合“纯数”的定义. 因此两位数的自然数中“纯数”有：10，11，12，20，21，22，30，31，32，共9个，而100显然也是“纯数”.综上所述，不大于100的“纯数”的个数共有：3+9+1=13个.

该解法在进行分类讨论时学生容易出现漏解的情况，特别是一位数0、1、2，以及三位数100.也有出现多解的情况，如13，23，33，所以计算时谨慎细心，分类时不重不漏.

解法二根据所给范围进行枚举

由于题目所给的取值范围为不大于100的数，而纯数的定义中又要求是自然数，所以学生可以将范围锁定在100以内(含100)的自然数，从而进行逐一列举，依次列出来符合条件的有：0,1,2,10,11,12,20,21,22,30,31,32,100，所以共有13个.

该解法简单易想，可操作性较强，但是比较耗费时间，而且很容易误判.

解法三根据各数位的可能取值进行排列组合

由于范围限定在100以内，可以先研究小于100的数中符合定义的，根据纯数不进位的要求，十位数字可选0，1，2，3，个位数字可选0，1，2，所以共4×3=12个，再加上三位数只有100一个数，因此总个数为12+1=13个.

该解法较为简洁，运用乘法原理与加法原理，可以快速算出纯数的个数，但是技巧性较强，多数学生不易掌握.

解法四画树状图进行分类列举

学生可以根据题意推断出百位数字可以是0，1，十位数字可选0，1，2，3，个位数字可选0，1，2，那么便可以使用初中统计学中画树状图的方法来进行列举.

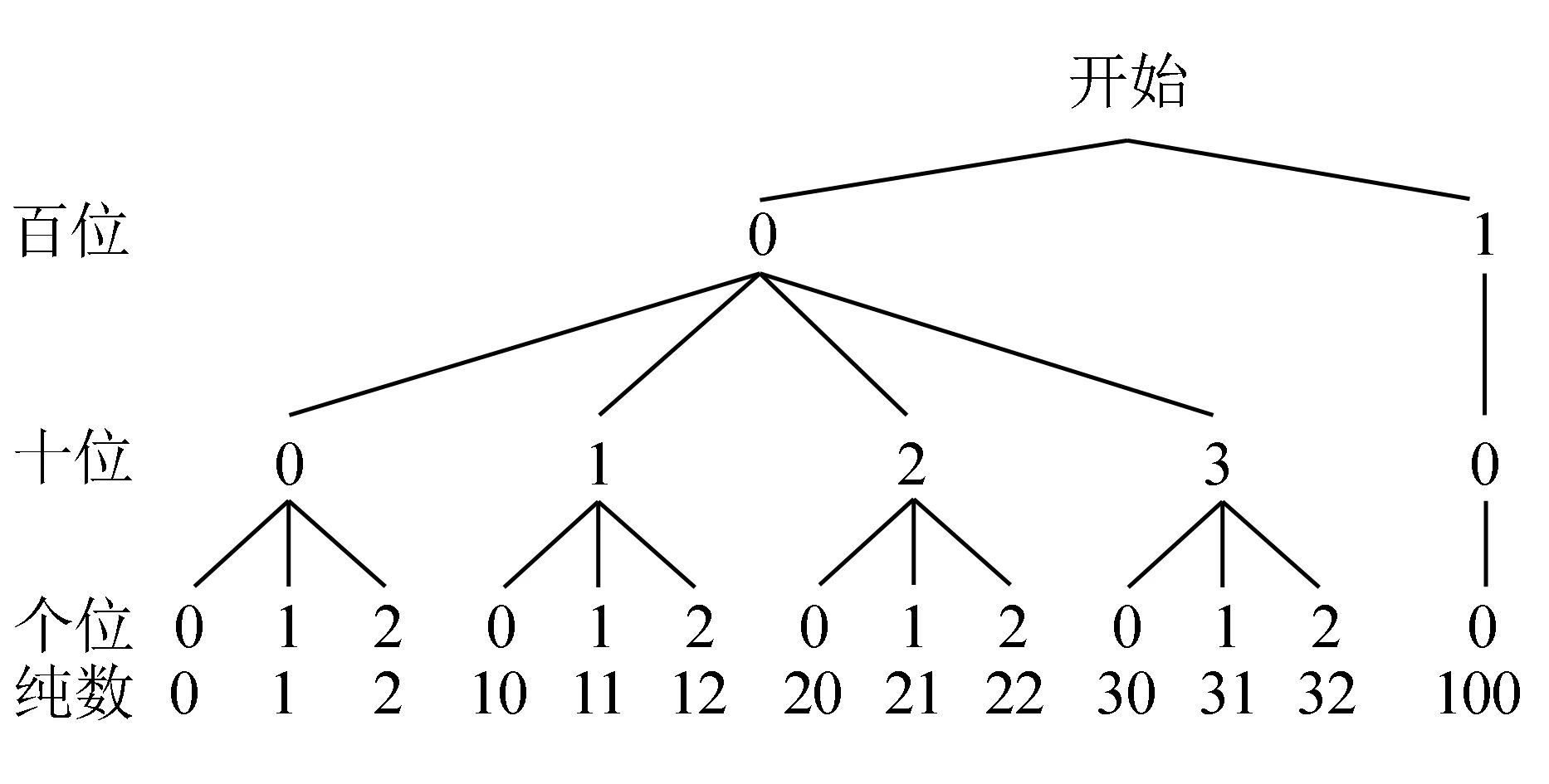
该解法非常巧妙，用统计学的知识来解决阅读理解问题，体现数学知识的灵活运用，又能体现分类讨论的不重不漏.

解法五综合使用上述解法

在实际解题过程中，学生的思维往往是发散的，所呈现的过程也未必恰好是某一种解法，所以混合使用多种解题方法，也能完美解决该题.例如在讨论两位数的纯数时，可以选择乘法原理或树状图，再将一位数和三位数中的纯数进行列举.

该解法比较灵活，学生比较常用，综合各解法之优势，仍需注意分类讨论的不重不漏.

4 策略反思

结合著名数学家波利亚在《怎样解题》中对解题的思维研究，以及近几年全国各地中考试题中阅读理解题目的解题经验，并根据上面对2019年重庆市中考数学A卷第22题阅读理解的分析过程，可以归纳出解决阅读理解问题的基本思路是“阅读→分析→理解→解决问题”，解题过程需要特别注意以下几点：

第一，理解材料——明确条件、原理、方法、结论.认真阅读材料，把握题意，注意一些数据、取值范围、关键名词等.“定义新概念”：如“和谐数”“完美数”“幸福数” 等；“定义新运算”的标志性语言 ：记为，规定，记作等；还要特别注意字母的取值范围或者定义本身要求的整数或自然数等.

第二，重视举例——检验是否理解正确，归纳主要方法.全面分析材料，理解材料所蕴含的基本概念、原理、思想和方法，提取有价值的数学信息.对于题目所给示例需要特别，示例中的方法是材料思想方法的重要体现，里面所含的解题方法或思想也极有可能是后面探究题目所需的.

第三，类比应用——结合数学思想方法解决问题.对有关信息进行归纳、整合，并且和方程、不等式、函数或几何等数学模型相结合来解答.用所学的内容来解决未学过的内容，体现了转化与化归的数学思想. 在进行模仿与创造时，要紧扣定义，结合示例，充分展现“阅读理解”的能力要求.