2021年高考全国乙卷压轴题

理科数学

12． 设 ，，，则（　　　）

A．

B．

C．

D．

答案　　B．

解析　　设 ，，，则

我们先需要判断 在 处的大小关系．考虑利用导函数研究三个函数的增长速度，有

注意到当 $0<x<2$ 时，有<="" p="">

因此

从而

16． 以图 ① 为正视图，在图 ②③④⑤ 中选两个分别作为侧视图和俯视图，组成某个三棱锥的三视图，则所选侧视图和俯视图的编号依次为＿＿＿＿＿（写出符合要求的一组答案即可）．

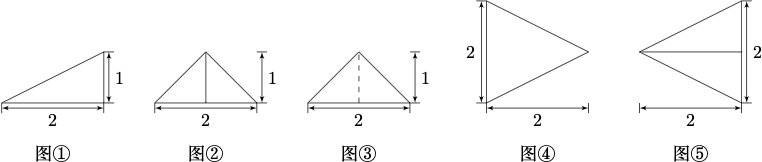
答案　　②⑤或③④．

解析　　如图．

20． 设函数 ，已知 是函数 的极值点．

（1）求 ．

（2）设函数 ，证明：．

答案　　（1）；

（2）略．

解析　　（1）令 ，则其导函数

根据题意，有

经检验，符合题意，因此 ．

（2）根据题意， 且 ，并且当 时，；当 $0<x<1$ 时，$f(x)="\ln" (1-x)<0$，于是题中不等式即<="" p="">

令 ，则 且 ，于是待证不等式即

根据基本放缩，该不等式成立，因此原命题得证．

21． 已知抛物线 （）的焦点为 ，且 与圆 上点的距离的最小值为 ．

（1）求 ．

（2）若点 在 上， 是 的两条切线， 是切点，求 面积的最大值．

答案　　（1）；

（2）．

解析　　（1）根据题意，有

（2）设 ， 且 ，则

从而 ，进而

根据三角形面积坐标公式， 的面积

由于 点圆 上，因此

记 ，，则有

因此

再设 ，，则

因此当 时， 取得最大值 ，此时 的面积取得最大值，为 ．

文科数学

12． 设 ，若 为函数 的极大值点，则（　　　）

A．

B．

C．

D．

答案　　D．

解析　　考虑到 ，因此在 的左右邻域 函数值均为负数，从而

16． 见理科数学第 题．

20． 已知抛物线 （）的焦点 到准线的距离为 ．

（1）求 的方程．

（2）已知 为坐标原点，点 在 上，点 满足 ，求直线 的斜率的最大值．

答案　　（1）；

（2）．

解析　　（1）根据题意，焦点 到准线的距离 ，因此 的方程为 ．

（2）根据题意有 ，设 ，则

因此直线 的斜率

等号当 时取得，因此所求斜率的最大值为 ．

21． 已知函数 ．

（1）讨论 的单调性．

（2）求曲线 过坐标原点的切线与曲线 的公共点的坐标．

答案　　（1）记 ，．当 时， 在 上单调递增；当 时， 在 单调递增，在 单调递减，在 单调递增；

（2） 和 ．

解析　　（1）根据题意，函数 的导函数

其判别式 ．

情形一　　当 时，，此时对任意 都有 ，所以 在 上单调递增．

情形二　　当 时，，此时 有两个互异实根，分别记为

当 时，；当 时，；当 时，．所以 在 单调递增，在 单调递减，在 单调递增．

（2）设切点坐标为 ，则切线方程为

代 入上式，可得

因此切线方程为

进而由

可知，．

因此所求公共点的坐标为 和 ．