北美大厂8月第一周算法面试真题汇总

题目描述：Remove Invalid Parentheses

Input: s = "()())()"
Output: ["(())()","()()()"]

Input: s = "(a)())()"
Output: ["(a())()","(a)()()"]

Given an integer array nums and two integers lower and upper, return the number of range sums that lie in[lower, upper]inclusive.

Range sum S(i, j) is defined as the sum of the elements in nums between indices i and j inclusive, where i <= j.

Example 1 :

Input: nums = [-2,5,-1], lower = -2, upper = 2
Output: 3
Explanation: The three ranges are: [0,0], [2,2], and [0,2] and their respective sums are: -2, -1, 2.

Example 2:

Input: nums = [0], lower = 0, upper = 0
Output: 1

题 解

这题可以使用前缀和+归并排序的解法实现更加容易理解；

这边介绍树状数组解法，详情见注释，利用树状数组记录的是具体某一个值得个数，快速求得小于等于某值的所有个数总和。

参 考 代 码

class Solution {
  static class BinaryIndexedTree {
    private final int[] data;
    private final int size;
    public BinaryIndexedTree(int size) {
      data = new int[size];
      this.size = size;
     }

    /**
     * BIT indexes: [0, 1, 2, ..., pos, pos + 1, ..., size - 1]
     *                ↑
     *            update position
     */
    public void update(int pos, int delta) {
      pos += 1;
      for (int i = pos; i <= size; i += i & -i) {
        data[i - 1] += delta;
       }
     }

    /**
     * BIT indexes: [0, 1, 2, ..., pos, pos + 1, ..., size - 1]
     *        ↑        ↑
     * query range:[left      right]
     */
    public int query(int pos) {
      pos += 1;
      int result = 0;
      for (int i = pos; i > 0; i -= i & -i) {
        result += data[i - 1];
       }
      return result;
     }
   }
  public int countRangeSum(int[] nums, int lower, int upper) {

    // construct the sums array
    long[] sums = new long[nums.length + 1];
    sums[0] = 0;
    for (int i = 0; i < nums.length; i++) {
      sums[i + 1] = sums[i] + nums[i];
     }

    // prepare sorted sums for numberToIndex
    long[] sortedNumbers = Arrays.copyOf(sums, sums.length);
    Arrays.sort(sortedNumbers);

    int result = 0;
    BinaryIndexedTree BIT = new BinaryIndexedTree(sortedNumbers.length);
    // 遍历的顺序是有sum[i]遍历，因此在以sum[i]为基础计算的时候，sum[i]之前的元素已经被更新到BIT中
    // 基于排好序的sortedNumbers的下标建立树状数组
    // 树状数组中 data[i] 表示数组 sum 中已经加入到BIT中的元素小于等于sum[i] 的个数有data[i]个
    for (int i = 0; i < sums.length; ++i) {
      // 区间值要在 [lower <= sum[i] - sum[?] <= upper]
      // 因此 sum[?] <= sum[i] - lower sum[?] >= sum[i] - upper
      // 所以小于等于 sum[i] - lower 的个数，减去 sum[i] - upper - 1 的个数，就是符合条件的个数
      result += BIT.query(numberToIndex(sortedNumbers, sums[i] - lower)) - BIT.query(numberToIndex(sortedNumbers, sums[i] - upper - 1));
      // 更新树状数组当中关联位置都 + 1
      BIT.update(numberToIndex(sortedNumbers, sums[i]), 1);
     }
    return result;
   }

  /**
   * find the last element no larger than `target`
   */
  public int numberToIndex(long[] sortedNumbers, long target) {
    int start = 0, end = sortedNumbers.length - 1;
    while (start + 1 < end) {
      int mid = start + (end - start) / 2;
      if (sortedNumbers[mid] <= target) {
        start = mid;
       } else {
        end = mid;
       }
     }
    if (sortedNumbers[end] <= target) return end;
    if (sortedNumbers[start] <= target) return start;
    return -1;
   }
}

Given `n` orders, each order consist in pickup and delivery services.

Count all valid pickup/delivery possible sequences such that delivery(i) is always after of pickup(i).

Since the answer may be too large, return it modulo 10^9 + 7.

Input: n = 1
Output: 1
Explanation: Unique order (P1, D1), Delivery 1 always is after of Pickup 1.

Input: n = 2
Output: 6
Explanation: All possible orders: 
(P1,P2,D1,D2), (P1,P2,D2,D1), (P1,D1,P2,D2), (P2,P1,D1,D2), (P2,P1,D2,D1) and (P2,D2,P1,D1).
This is an invalid order (P1,D2,P2,D1) because Pickup 2 is after of Delivery 2.

题 解

每一个物品有取货送货两个操作，且送货必须在取货之后；针对于 n 个物品，最终一工会产生 2 * n 个操作。若此时再加入第 n + 1 个物品，相当于多了 2 步操作，我们需要计算的是这 2 步操作可以穿插在哪些操作中。很容易通过推导得出取货操作可以穿插在 2 * n + 1 个地方，对应每一种穿插位置，送货穿插的位置依次为 1, 2, 3, 4, ....., 2 * n + 1。

参 考 代 码

class Solution {
  public int countOrders(int n) {
    int mod = 1000000007;
    long[] dp = new long[n + 1];
    if (n == 1) {
      return 1;
     } 
    if (n == 2) {
      return 6;
     }
    dp[1] = 1L;
    dp[2] = 6L;
    // 推导公式
    for (int i = 3; i <= n; i++) {
      int insertPoints = (i - 1) * 2 + 1;
      // 当前新加入的物品可以穿插的取货送货的组合数
      long count = (1 + insertPoints) * insertPoints / 2;
      dp[i] = (dp[i - 1] * count) % mod;
     }
    return (int)dp[n];
   }
}

题目描述：Number of Good Leaf Nodes Pairs

Given the root of a binary tree and an integer distance. A pair of two different leaf nodes of a binary tree is said to be good if the length of the shortest path between them is less than or equal to distance.

Example 1 :

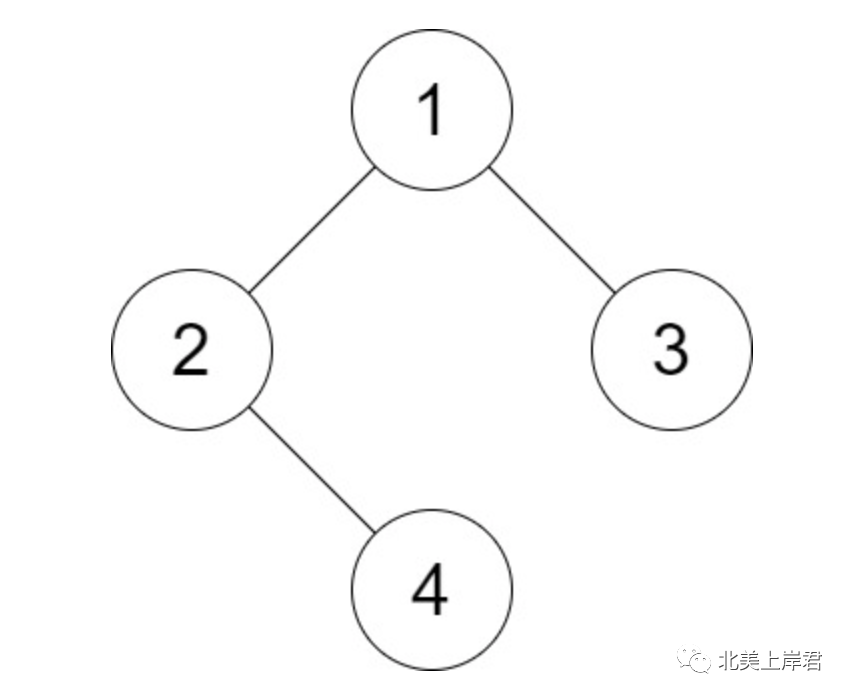
Input: root = [1,2,3,null,4], distance = 3
Output: 1
Explanation: The leaf nodes of the tree are 3 and 4 and the length of the shortest path between them is 3. This is the only good pair.

Example 2 :

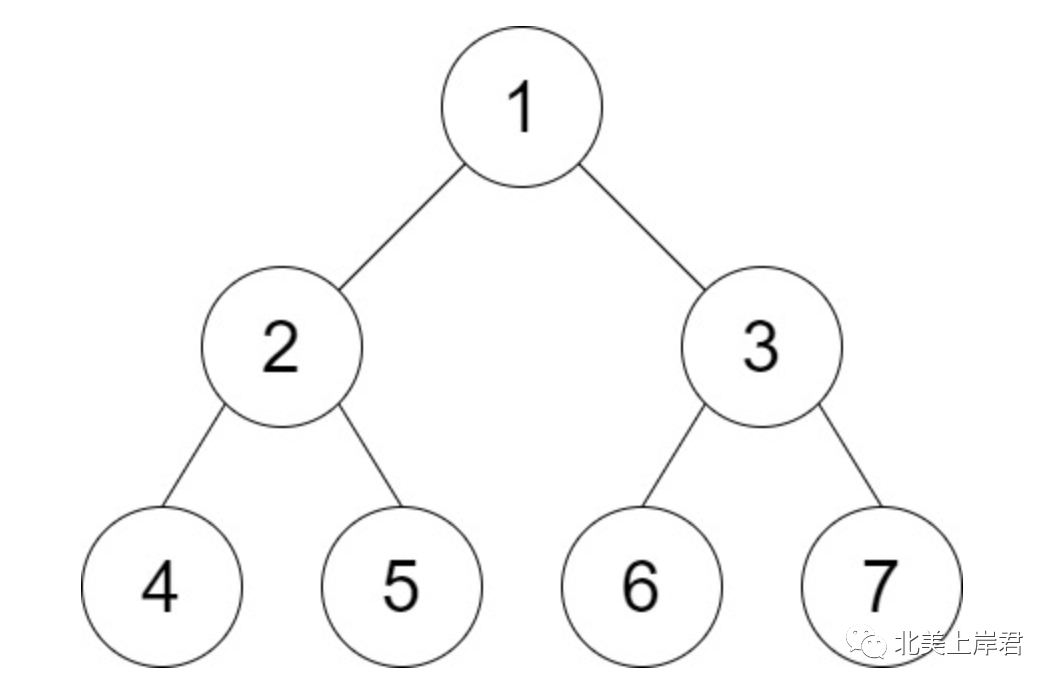
Input: root = [1,2,3,4,5,6,7], distance = 3
Output: 2
Explanation: The good pairs are [4,5] and [6,7] with shortest path = 2. The pair [4,6] is not good because the length of ther shortest path between them is 4.

题 解

分治法计算当前距离当前root节点的叶子节点满足条件的个数，若距离当前叶子节点距离为 L1 的左子树叶子节点个数有 n 个，右子树距离当前节点为 L2 的叶子节点个数有 m 个，若 L1 + L2 < d，则有效的叶子对为 n * m。使用 Map 来记录当前 root 节点左右子树的叶子节点距离及个数信息。

参 考 代 码

class Solution {
  int res = 0;
  public int countPairs(TreeNode root, int distance) {
    if (root == null) {
      return 0;
     }
    dfs(root, distance);
    return res;
   }
  
  private Map<Integer, Integer> dfs(TreeNode node, int d) {
    Map<Integer, Integer> disToCount = new HashMap<>();
    if (node == null) {
      return disToCount;
     }
    if (node.left == null && node.right == null) {
      disToCount.put(1, 1);
     }
    // divide 分别计算左右子树的距离和节点个数信息
    Map<Integer, Integer> leftInfo = dfs(node.left, d);
    Map<Integer, Integer> rightInfo = dfs(node.right, d);
    // conquer 在满足距离的情况下计算合法的叶子对数
    for (int lDis : leftInfo.keySet()) {
      for (int rDis : rightInfo.keySet()) {
        if (rDis <= d - lDis) {
          res += leftInfo.get(lDis) * rightInfo.get(rDis);
         }
       }
      // 若距离当前root节点的距离为超过 d - 1, 说明还能再往当前root的父亲走过，因此距离 + 1
      if (lDis + 1 < d) {
        disToCount.put(lDis + 1, leftInfo.get(lDis));
       }
     }
    // 右子树的判断也是一样
    for (int rDis : rightInfo.keySet()) {
      if (rDis + 1 < d) {
        // 这边因为Map中记录的当前root的父亲，因此对于当前的disToCount，记录的整个当前root的子树
        // 而有些距离在计算left的时候已经被更新过了
        disToCount.put(rDis + 1, rightInfo.get(rDis) + disToCount.getOrDefault(rDis + 1, 0));
       }
     }
    return disToCount;
   }
}

我们

杭州上岸算法网络科技有限公司

上岸算法网络科技有限公司是一家致力于用高质量，高互动性小班课程来帮助学生更好的在就业市场中定位以及求职的公司。我们以顶级的课程质量，高互动性的教学方式以及独特的小班教学模式来帮助学生更快的跨过求职的鸿沟，用最高效，经济，合理的方式帮助更多学生快速找到梦寐以求的工作。