gongzhong号，可在微信好友里自动收到每天的推送，还可以查看全部资源。
识别下面ErWeiMagongzhong号
七、八、九年级的童鞋们，每天都可以从这拿到一道数学题哦！知识强化、课外拓展、思维提升，都在这一道数学题里了。提醒大家：题目不简单，够胆来挑战！请认真答题，一定要坚持住哦！也欢迎邀请同学参与到我们的答题中哦！刷屏到文末，点击左下角“”可查看“7-9年级”全部课程。写出下列各单项式的系数和次数：
| 30a | ﹣x3 | y | ab2c3 |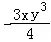 
| πr2 |
系数 |
|
|
|
|
|
|
次数 |
|
|
|
|
|
|
【答案】
【解答】：
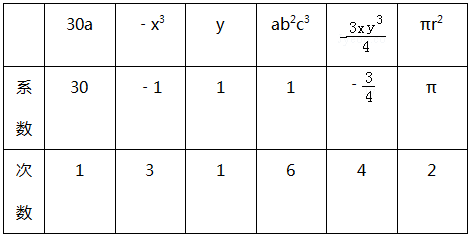
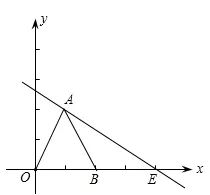
如图,△OAB是边长为2的等边三角形,过点A的直线△OAB与x轴交于点E.
（1）求点E的坐标.
（2）求证:OA⊥AE。
【答案】
【解答】：
（1）过点A作AD⊥EO于点D,∵△OAB是边长为2的等边三角形,∴OD=DB=1，AB=AO=OB=2，∴AD=
,∴A（1，
）,
将A点代入直线
得:
，
∴
∴
，
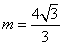
∴E(4，0)
（2）证明：
∵AD=
,DE=EO-DO=3，∴AE=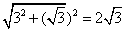
∵AO2+AE2=16，EO2=16
∴AO2+AE2=EO2,
∴OA⊥AE
如图,△OAB是边长为2的等边三角形,过点A的直线△OAB与x轴交于点E.
（1）求点E的坐标.
（2）求证:OA⊥AE。
【答案】
【解答】：
（1）证明：∵PQ⊥AQ，
∴∠AQP=90°=∠ABC，
在△APQ与△ABC中，
∵∠AQP=90°=∠ABC，∠A=∠A，
∴△AQP∽△ABC．
（2）解：在Rt△ABC中，AB=3，BC=4，由勾股定理得：AC=5．
∵∠QPB为钝角，
∴当△PQB为等腰三角形时，
（I）当点P在线段AB上时，如题图1所示．
∵∠QPB为钝角，
∴当△PQB为等腰三角形时，只可能是PB=PQ，
由（1）可知，△AQP∽△ABC，
∴
，即
，解得：PB=
，
∴AP=AB﹣PB=3﹣
=
；
（II）当点P在线段AB的延长线上时，如题图2所示．
∵∠QBP为钝角，
∴当△PQB为等腰三角形时，只可能是PB=BQ．
∵BP=BQ，∴∠BQP=∠P，
∵∠BQP+∠AQB=90°，∠A+∠P=90°，
∴∠AQB=∠A，
∴BQ=AB，
∴AB=BP，点B为线段AP中点，
∴AP=2AB=2×3=6．
——END——
来源：本文内容来源于网络，我们尊重原创，如有侵权联系删除。
相关资源