当我们谈论数学时,我们在谈论什么?
发布于 2021-09-03 13:40 ,所属分类:数学资料学习库
1 数学研究的对象
数学是人们追求简单化而产生的. 早期的人类以打猎为生,为了计算猎物的数量,他们用石刀在树上刻痕或结绳计数. 一个刻痕或者一个绳结代表一个猎物,从单个个体可以抽象出了数字“1”的概念. 形成了数字“1”的概念后,1就不再具体的表示一种猎物了. 可以是一头狮子,也可以是一头麋鹿,还可以是一棵树,当然也可以是一个人、一座山、一个苹果……关于数字“1”具体的例子,生活中比比皆是,而数学中抽象化的“1”只存在于人的头脑中. 再看加法和减法的产生. 让我们想象一下,一个原始人两天打猎的生活. 昨天打来的猎物没有吃完,今天又阳光明媚,万里无云的,真真是个外出捕猎的好日子. 猎物增加了,就产生了加法. 美滋滋地睡了一觉后,第二天发现,我的妈呀,外面雷电交加、疾风骤雨,吓死我这个原始人了. 不行,不行,今天不能打猎了,就吃昨天打来的吧. 猎物减少了,于是产生了减法…… 这是数学研究的第一类对象:数量关系.
早期的数学发展是和人类实际生活息息相关的. 农耕文明时期,种植和收获庄稼是人们赖以生存的主要手段. 种植需要土地,而丈量土地是当时的人们不得不解决的问题. 比如说如何把一块长方形、三角形、平行四边形的土地平均分成两块,一半种玉米,一半种大豆. 当时的人们不像现代人类,拥有皮尺、卷尺和测量仪等工具,无法知道用来种植的土地有多长、多宽. 但是人类的智慧是无穷的,当时具有数学家头脑的人想出了如何画出一个直角、找出一条线段的中点、求出一个角等于已知角、将已知角划分为两个相等的角等等的办法. 这样,人们就可以把一块长方形、三角形、平行四边形的土地划分为相等两部分,或者再划分出一块新的土地和原来的土地面积相等. 注意,以上的一切都是没有用到度量的,也就是说当时的人们是没有刻度尺的. 这就开辟了数学一个全新的领域,像这种没有数字(度量)的数学,我们称之为几何. 前面说的都是在一条直线或同一个平面里面进行的几何研究,是一维和二维的空间. 人类生存的空间是三维的立体空间,不仅有平面图形,还有很多立体图形. 而数学中许多在低维空间成立的命题,推广到更高维也是成立的. 这就是数学研究的第二类对象:空间形式.
数学研究的第三类对象,或者说是研究对象的统称:模式结构.数学家哈代曾经说过:“一位数学家就像一位画家或诗人,是模式的创造者.如果他的模式比画家或诗人的模式的生命更加长久的话,那是因为他的模式是用思想所创造的.”这里的“模式”含义十分广泛.首先,它当然包括前面提到的数量关系和空间形式,而且还包括数学抽象后的各类模型和结构.数学是关于模式的科学,而大自然中的模式应有尽有.[1]虽然关于数学是发明还是发现的争论不休,但这并不妨碍我们使用数学整理宇宙间的规律,使其简单明了. 倘若宇宙中真的存有外星文明,他们有着和我不同的模样,讲着不同的语言,怎样才能和他们交流呢?答案是使用数学. 数学将作为一种语言,搭建起与外星文明沟通的桥梁. 地球上早期的各个文明互不交流,无法沟通,数学上却能取到相同的成果. 如勾股定理也叫作毕达哥拉斯定理,是因为在中国和希腊的数学家都独立的发现了:在直角三角形中,两直角边长的平方和等于斜边长的平方. 事实上,勾股定理就曾被选定作为媒介,向外星人传达信号,其他地方存在数学文明,并发展到了一定程度. 如此看来,数学是开启宇宙之门的钥匙.

2 诗意的数学世界
数量关系的大厦是从自然数“1”开始的,而空间形式的大厦是从“点”开始的. “1”和“点”在现实生活中是不存在的,它们只存在于人的头脑中,是抽象的.小学毕业后计算1+2=3,你想到的还是一个苹果加上两个苹果等于三个苹果吗?不是的. 你能在现实生活中找到一个数学中定义的完美的圆吗,能找到一个完美的球?是不可以的.这是因为,经历从现实世界抽象出数量关系、空间形式和模式结构的过程后,数学世界已经是有别于现实世界的另一个世界了. 就像作家王小波说的:“一个人只拥有此生此世是不够的,他还应该拥有一个诗意的世界.”在我看来,数学就是这样一个诗意的世界,数学来源于实际却高于实际,一旦进入数学世界,并不一定非要处处联系实际.数学世界的画卷正在展开……

太极分两仪,正义与邪恶势不两立,美丽与丑陋是对立的,光明与黑暗界限分明……似乎事物总有两面性.在数学世界却不尽然. 莫比乌斯环就是只有一面的环. 你只需要将一张长方形的纸旋转180度,再对接两头,就可以轻松的制作出一个莫比乌斯环. 克莱因瓶是另一个例子. 在我们的生活中,似乎所有的器皿,如瓶子、杯子、茶壶等都有内部和外部之分. 数学世界中的克莱因瓶是没有内外之分的,或者说内部就是外部,外部就是内部.


问题一:现有煤气灶、自来水龙头、空水壶摆在您面前. 当您要烧开水时,您应当怎么做呢?
问题一的答案是,将水壶注满水,点燃煤气,将水壶放在煤气灶上,等待.
问题二:现有煤气灶、自来水龙头、注满水的水壶摆在您面前. 当您要烧开水时,您应当怎么做呢?
数学家的回答是:将壶中的水倒掉!
这样,问题二就变成问题一了. 这正是数学的可爱之处,也正是数学中的化归、等价转换思想,总是把未解决的问题转化成已经解决的问题.
3 数学之美
数学有简洁之美. 数学本就是人类为追求简单化而产生的. 数学家们通过抽象的方法,过滤掉事物的感性属性,还原这个世界最本质的特征,以便于更好的认识和改造这个世界. 比如说,从现实世界中抽象出的几何图形的过程是忽略掉了事物的物理、化学等属性,抽象出长方形、三角形、正方体、圆柱等等,只物体的形状、大小和位置. 抽象出这几类图形后,人们就可以自由地组合、变形,添加感性的属性后,再还原到现实世界,就可以创造新的事物了. 这还不算完,几何图形进一步可以拆解为点、线、面,这是简化之后的再简化. 因此,对复杂的现实世界的研究可以归结为对一些基本图形的研究,而对一些基本图形的研究又可以归结为研究点与点、点与线、线与线、线与面等之间的关系. 简直精彩至极.
数学有精确之美.直线与圆相切,意味着直线与圆仅相交于一点. 点是没有大小的,相交于一点,人的眼睛是无法分辨的. 数学精确到可以解决微观的粒子问题.

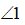 和
和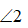 互为对顶角,
互为对顶角,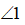 和
和 似乎一看就是相等的. 数学家却不相信这种直觉,《几何原本》中欧几里得对“对顶角相等”做了严格的证明. 这也是初中生遇到的第一个被严格证明的命题. 这是启迪中学生数学严谨性的开端. 世界上没有纯粹理性的人,人都是感性. 生活中,人们相信“眼见为实”或者将自己既定的“想法”当成了的事实,从而看不见真相,造成了多少误会. 数学的严谨性是代表人类理性的那一面.
似乎一看就是相等的. 数学家却不相信这种直觉,《几何原本》中欧几里得对“对顶角相等”做了严格的证明. 这也是初中生遇到的第一个被严格证明的命题. 这是启迪中学生数学严谨性的开端. 世界上没有纯粹理性的人,人都是感性. 生活中,人们相信“眼见为实”或者将自己既定的“想法”当成了的事实,从而看不见真相,造成了多少误会. 数学的严谨性是代表人类理性的那一面.
数学的举反例思想更是无与伦比,如何反驳“世界上所有的天鹅都是白色的”,仅需要找到一只黑天鹅即可.但是举不出反例,并不代表该命题是正确的. 哥德巴赫猜想至今举不出一个反例,但因为未被严格证明,所以不能被认为真正意义上的正确.
数学有概括之美.数学抽象只是数学的方法和过程,抽象是过程,概括是结果. 概括性是数学的大杀器,往往能以有限的模式驾驭无穷的具体. 我们只要给定了一个数学概念的定义,就是概括性的体现. 例如三角形的定义:“三角形是由同一平面内不在同一直线上的三条线段‘首尾’顺次连接所组成的封闭图形. ”三角形有大有小,大的可以大到地球都放不下,小的可以小到用显微镜才能看到. 但是,只要一个平面图形满足上面的三角形定义,它就是三角形. 再如,平面向量基本定理. 平面上有多少个向量?向量有长有短,长至十万八千里,短至1纳米,还有无穷无尽的方向,这么多无穷无尽的向量如何掌控......对于平面上任意一个非零向量,在这个平面上随意选定两个不共线的向量i, j,分别过起点A和终点B作直线a平行于i, 直线b平行于j, 因为i和j不共线, 所以直线a, b必然交于一点, 根据向量的三角形法则和数乘向量就可得出 [2]这么多无穷无尽的向量居然可以只用两个不共线的已知向量i和j线性表示.
[2]这么多无穷无尽的向量居然可以只用两个不共线的已知向量i和j线性表示.
数学有统一之美.代数和几何是统一的. 实数和数轴上的点可以建立一一对应的关系. 曲线上点的坐标和方程的解可以统一起来. 一元二次方程、一元二次不等式统一在二次函数. 椭圆、双曲线、抛物线统一成圆锥曲线. 正因为数学是这样充满联系的整体,学会用不同的眼光看问题,会得到意想不到的结果. 比如说, 都是实数,并且
都是实数,并且 试求
试求

的最小值[3]. 如果从代数的角度看,可以运用实数绝对值定义,分类讨论打开绝对值号. 还可以先从代数角度考虑,直接把

看作一个分段函数,然后结合函数图像求最小值. 但是,这两种方法,
代数的运算过程都十分繁琐. 如果我们直接以数轴作为思维工具,明白 不过就是表示点x和点a之间的距离,
不过就是表示点x和点a之间的距离,
不过就是表示点x到点a,b,c的距离之和. 这道题立马变得太简单了!
4 数学的欣赏
 常常被誉为数学中最美妙的一个公式,复数范围内最重要的5个数
常常被誉为数学中最美妙的一个公式,复数范围内最重要的5个数 竟然这么和谐的相处在同一个等式中. 这种感觉就像是你最喜欢的5个电影明星竟然同框出现在同一部电影中,并且都贡献了精彩的演出;这种感觉也像是你竟然收集了5个最爱的奥特曼手办,那一刻你变成了光;这种感觉还像是你竟然集齐了散落各处的七龙珠,成功召唤神龙.
竟然这么和谐的相处在同一个等式中. 这种感觉就像是你最喜欢的5个电影明星竟然同框出现在同一部电影中,并且都贡献了精彩的演出;这种感觉也像是你竟然收集了5个最爱的奥特曼手办,那一刻你变成了光;这种感觉还像是你竟然集齐了散落各处的七龙珠,成功召唤神龙.

再看陈子昂的诗:“前不见古人,后不见来者. 念天地之悠悠,独怆然而涕下. ”从数学的角度来欣赏这首诗:诗人以自己所在的时间点为原点,前不见古人是时间轴的负无穷,后不见来者是时间轴的正无穷,念天地之悠悠是诗人生存的三维空间. 时间轴和三维空间不正是爱因斯坦的四维时空吗.[4]穿越古今,宇宙无穷,感时伤怀,妙不可言. 这是爱好文学和爱好数学之人可以共通的意境.
5 结语
或许你还感受不到上面所说的数学之美,或许你赞同“数学学到加减乘除就够了”这样的观点,或许你一听到数学这两个字想到的是“各种枯燥的符号公式和无休无止的计算”,或许你认为自己一辈子都不会用到数学,或许你知道数学很有用但实在不喜欢数学,或许你知道数学很有用但说不上用在哪里,或许……何不“让子弹飞一会”,金庸先生的小说《倚天屠龙记》中张无忌小时候住在冰火岛,他的义父谢逊逼迫他背下许多武功要诀,还说“虽然你现在不懂,但先记着,将来总会懂的”. 数学就类似那些武功要诀,初学不解其中味,只觉得痛苦和枯燥. 等烂熟于心后,慢慢地理解了,才感受到其中的妙处. 所以欣赏数学的前提是理解数学. 没有理解才会有伤害,才会有“数学无用论”. 艺术欣赏里文字有情,音乐有声,绘画有色……数学欣赏却不同于以上艺术,数学是精确、严谨、概括、统一、简洁的,有自己独特的美感. 正如数学家莫里斯·克莱因所说:“音乐能激发或抚慰情怀,绘画使人赏心悦目,诗歌能动人心弦,哲学使人获得智慧,科学可改善物质生活,但数学能给予以上的一切. ”如此美妙的学科,何不试着去学习它、理解它,进一步感受它无与伦比的魅力.
如果有一天,地球面临毁灭,世界上的书籍即将焚烧殆尽. 你的面前摆着两本著作:欧几里得的《几何原本》和莎士比亚的《悲喜剧精选》,只能将一本书带到人类生存的另一个星球,你会选哪本?我的选择是《悲喜剧精选》,理由倒不是人类进入另一个星球生存后,更需要精神文明的延续.不选择《几何原本》的原因仅仅是:没有必要.数学因追求简单化而产生,以思维为基础创造模式,模式再生模式,思维不死,数学不灭. 只要宇宙中还有一根会思考的芦苇,数学就永远不会消亡.
欢迎来到精彩的数学世界.
参考文献
[1]胡典顺.数学究竟是什么[J].数学教育学报,2011,20(01):76-79.
[2]何小亚.数学:大道至简,驾驭无穷[N].人民日报海外版,2020-09-28(9).
[3]孙维刚. 孙维刚初中数学[M]. 北京:北京大学出版社, 2015.
[4]张奠宙. 数学教育纵横[M]. 广西:广西教育出版社,2019.


























相关资源