考研数学学习如何抓定义?如何扎实基础?

在学习数学的过程中经常听人说“基础不牢，地动山摇”，“死扣定义”等一些词眼，那应该如何打基础，如何扣定义呢？很多同学也都说，自己在数学的复习过程中也没少看定义，课本也看过好多遍了，为什么还是做题不会，公式不查书不放心，书上的一些题型的解读明明很清晰明了但是就是不明白…所以今天就拿李范全书（只限第一章一部分知识点）为例，说一下我对“基础，定义”，在学习的过程中我是怎么学的，怎么理解的，希望对学习数学有迷惑的同学一些启发（因为我是完全自学的，没有跟老师，所以对于有些知识点的理解可能做不到特别透彻，有所启发就足够了）。

• 关于极限的定义

首先极限包括数列极限和函数极限，数列极限是函数极限的一种特殊的情况，数列的下标只可以取正整数（这就是为什么上面写的函数极限的定义1.2比数列极限定义1.1多加了一个绝对值）。那极限是什么呢？“极限”的定义，就是为了绕过用一个数除以0的麻烦，引入了一个过程的任意小量（就是说，除数不是零，所以就有意义，同时这个过程小量可以取任意小，它只要满足在区间内，都小于该任意小量，那极限就是该数），这个数存在极限那就收敛，不存在极限就发散喽。

所以有了这样的背景，就出现了“极限的这种语言描述，以下是它的名字“

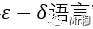
这个语言描述是特别重要的，很多同学只知道如下这样表示极限的写法

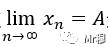
却忽略了它的语言描述，所以在学习极限的定义的过程中，你要熟练掌握极限的写法和它对应的语言描述（就是说它的语言你要理解，会熟练使用，看到类似就必须立刻可以反映出它的语言怎么说，细节有哪些，不可以错），至于怎么理解，你可以按照我上面写的那样，去理解它。

• 关于极限的基本性质

按照上面讲的极限的定义，那极限的基本性质的理解思路就该像下面这样了：

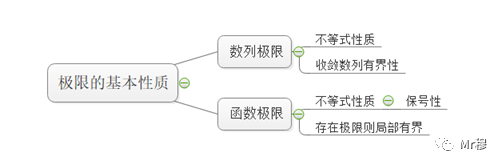
1.不等式性质：

数列极限：

按照给出的定理那样说的，对它表述的理解，不就是又使用了我们的极限的定义内容吗？也就是“极限的语言+不等式（得出的极限大的对应的数列就大，反之数列不管是大于还是大于等于，那对应的极限都是大于等于而不是大于）进行描述得出来的”。

那函数极限和数列极限，对于不等式性质也肯定是同样这样定义了，要理解了把它熟记，而函数极限另一个部分的不等式性质

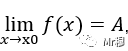
倘若和0做比较，那通过极限语言表达出来，就是极限的保号性了。

2.有界性质：

关于数列的有界性质，“数列收敛则有界”，学过极限的对这个都记的滚瓜烂熟了，但是光这个还不够，它所对应的“语言”更重要，记忆的方法就是理解了记，而如何理解前面早已经说过了。为什么说它更重要（也就是说一些定义的性质很重要，但是它所对应的语言会更重要），是因为一道题目尤其是证明题，你不仅要熟练的通过它给的某个关键词抓取出它可能要考察你的定义和性质，你还要想到性质后立刻可以用它对应的语言表达出来。我觉得这在打基础的过程中还蛮重要的，虽然很难也很费精力，但是这可以让你对它有更深的理解，可以掌握的更牢固。同样，存在极限的函数局部有界性，也是按照这样的思路去理解和记忆，至于为什么是空心邻域，是因为它是极限，是无限趋于但是不等于。

3.重要极限是很基础的知识点，要背过会用。但是，在以后求极限的过程中，相对来说我建议多用泰勒少用重要极限（尤其是A±B这样的极限），有时候某个题的极限是1/6，而你做出了1/2，你做错的原因就是因为你直接运用了重要极限，造成它的精度不够，使用泰勒一定要把握好泰勒精度，也就是要展开到第几项（有需要后续我可以发文章解答这里）

通过上面的讲解，希望大家可以对数学的定义和基础的学习有一点点启发了。接下来，还是利用前面的学习思路来对这一部分进行讲解，还是从数列极限和函数极限来讲，由此可见，数学的知识是连贯的，你要会进行系统的理解和学习。

一、极限存在的两个准则：

1.关于夹逼定理：就像上面你看到的这样，利用极限的语言和不等式性质，得出来的这两条，满足的话那它就有极限。定义就是图上面说的，你不要给人家乱改，如果和上面不一样，这时候你就得好好想想了，一般这时候就不满足夹逼定理了。比如660的这个题：

夹逼定理很重要，使用非常广泛，在一些综合题里经常用，这里我只说一个要注意的点。数列极限、函数极限均如此。

2.关于单调有界数列必收敛：这里你要知道单调上升有上界或者单调下降有下界，那就有极限，就肯定收敛（递归数列求极限就经常用到，这样的题也有一套方法）；要会用语言给它叙述，这些就够了。

极限存在的一个充要条件：

那这里又提到了极限，所以还是分别说函数极限和数列极限。函数极限：就是某个点左边有极限，右边有极限，左右极限相等，那就可以了（与在这个点处的值相不相等是没有关系的）数列极限：就是要涵盖它所有的，比如2n是图上写的这样的两项，换成3n你也要知道是哪三项。

二、证明极限不存在的方法

总的来说就是两条：第一条是函数极限，要利用极限存在的充要条件；第二条是数列极限，要满足涵盖的项要都相等，这里举一个容易忽视的例子。

写到这里，这样学习定义、学习基础的方法就是我之前用的了，第一章的内容很重要，尤其后面关于函数的连续性、连续函数的性质更是重要，这里就不再细说了。很多定义很多性质我当时学习的时候也并不顺利（千万不要简单的看一遍再去做一些题，就认为差不多了，差很多），我是利用晚上休息的时间去网上搜索各种不懂的知识点，去理解去体会，看了很多遍也背了很多遍，做了很多的题这样慢慢积累而来的。

数学的学习，哪怕是关于一个小的章节的学习，都不可能一蹴而就，要勤下功夫。基础要这样一步步的夯实，基础真的很重要，但同时题也不可以少做，有意义的题往往会给你带来灵感。学习数学的过程中，遇到了那种近一个小时都想不明白的题或者知识点，这时候建议跳过去继续走，不要钻牛角尖，利用碎片时间去琢磨，不然会耗费你大把的时间。

天才很少，我们都是很平凡却又不甘平凡的人。你所看到听到的一些传闻，那些动不动数学学了几遍，某某学校今年可能炸了，听说某某学校数二要改数一等一系列改革，真题达不到130+估计凉了，今年数学肯定特别难…这些不需要你去理会，说改革大家都一样，说难大家都难；学习的时候做到两耳不闻窗外事，打好基础，用适合自己的学习方法去学习，你我都会成功。