2021年浙江省嘉兴市中考数学压轴题解析

沉下去，才会浮起来！

先给gongzhong号求个！欢迎常来！

【真题再现】

23.已知二次函数y=-x²+6x-5.

(1)求二次函数图象的顶点坐标.

(2)当1≤x≤4时，函数的最大值和最小值分别为多少？

(3)当t≤x≤t+3时,函数的最大值为m,最小值为n,若m-m=3, 求t的值.

24.小王在学习浙教版九上课本第72页例2后，进一步开展探究活动：将一个矩形ABCD绕点A顺时针旋转α(0°＜α≤90°)，得到矩形AB´C´D´，连接BD.

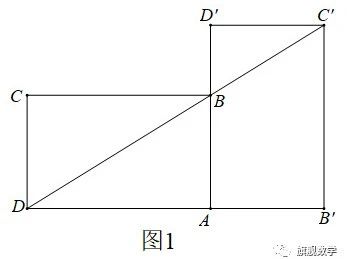
【探究1】如图1，当α=90°时，点C´恰好在DB延长线上.若AB=1，求BC的长.

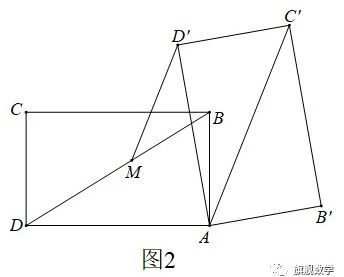
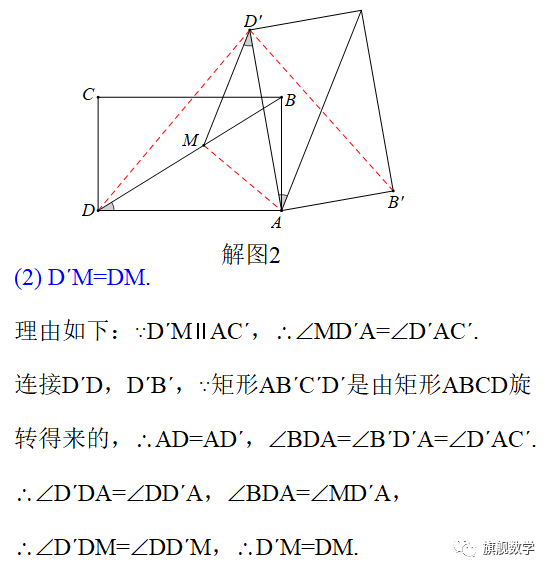
【探究2】如图2，连接AC´，过点D´作D´M∥AC´交BD于点M.线段

D´M与DM相等吗？请说明理由.

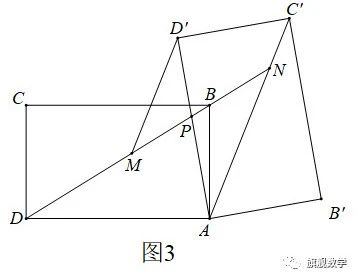
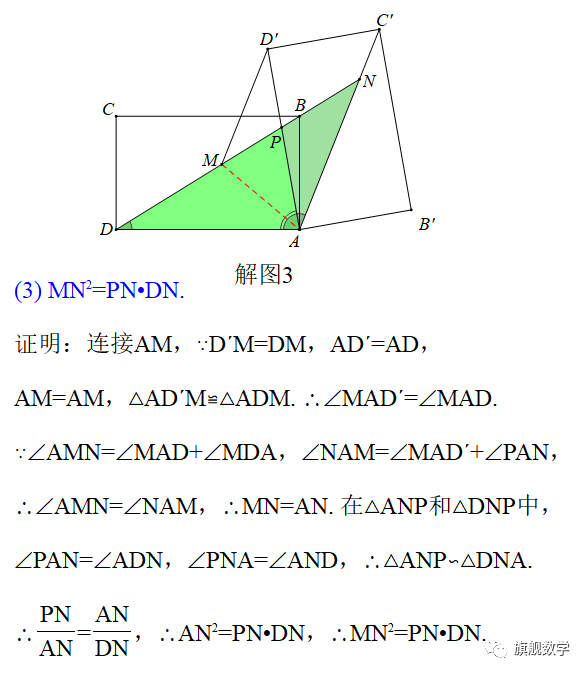
【探究3】在探究2的条件下，射线DB分别交AD´，AC´于点P，N(如图3)，发现线段DN，MN，PN存在一定的数量关系，请写出这个关系式，并加以证明.

【解题思路与参考解答】

23.

(1) ∵y=-x²+6x-5=-(x-3)²+4，∴该二次函数图象的顶点坐标为(3, 4).

(2)∵y=-x²+6x-5=-(x-3)²+4，∴该二次函数图象的对称轴为x=3，开口向下.∵1≤x≤4，∴当x=3时，函数取得最大值4；当x=1时，函数取得最小值0.

(3)①当t＞3时，y随x的增大而减小. ∴当x=t时，函数取得最大值m=-t²+6t-5；当x=t+3时，函数取得最小值n=-(t+3)² + 6(t+3) -5

=-t²+4.

∵m-n=3, ∴(-t²+6t-5)-(-t²+4)=3,

∴t=2(舍去).

②当t+3＜3，即当t＜0时，y随x的增大而增大. ∴当x=t时，函数取得最小值n=-t²+6t-5；当x=t+3时，函数取得最大值m=-(t+3)²+6(t+3)

-5=-t²+4. ∵m-n=3，∴(-t²+4)-

(-t²+6t-5)=3，∴t=1(舍去).

③ⅰ 当t≤3≤t+3, 且3-t＞(t+3)-3,即当0≤t＜1.5时, 则当x=3时, 函数取得最大值m=-3²+6×3-5=4,当x=t时, 函数取得最小值n=-t²+6t-5；

∵m-n=3，∴4-(-t²+6t-5)=3，t1=3+√3(舍去)，t2=3-√3.

ⅱ 当t≤3≤t+3，且3-t≤(t+3)-3, 即当1.5≤t≤3时, 则当x=3时, 函数取得最大值m=-3²+6×3-5=4, 当x=t+3时,

函数取得最小值n=-(t+3)²+6(t+3)

-5=-t²+4.

∵m-n=3，∴4-(-t²+4)=3，

t1=√3，t2=-√3(舍去).

综上所述，t的值为3-√3或√3.

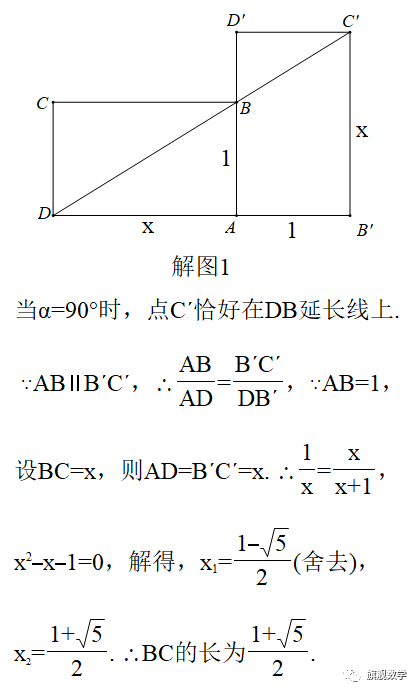
24.(1)

The End, Byebye!

旗舰数学与你一起畅游数海

敬请和“在看”