【每日一题】初中(7-9年级)数学培优提升(第38期答案)

七

多项式x^m﹣1﹣3x³﹣4是四次三项式，则m=　 　．

【答案】

5

【分析】：

由于多项式是关于x的四次三项式，根据以上两点可以确定m的值．

【解答】：

∵多项式是关于x的四次三项式，

∴m﹣1=4，

即m=5，

故答案为：5．

【点评】此题主要考查了多项式的定义，熟练根据多项式定义得出是解题关键．

八

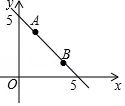
如图，已知一次函数y=mx+5的图象经过点A（1，4）、B（n，2）．

（1）求m、n的值；

（2）当函数图象在第一象限时，自变量x的取值范围是什么？

（3）在x轴上找一点P，使PA+PB最短．求出点P的坐标．

【答案】

【解答】：

（1）∵一次函数y=mx+5的图象经过点A（1，4），

∴m+5=4，解得：m=﹣1；

∵点B在一次函数y=﹣x+5的图象上，

∴﹣n+5=2，解得：n=3．

∴m、n的值分别是﹣1、3．

（2）当y=﹣x+5=0时，x=5，

∴一次函数y=﹣x+5的图象与x轴的交点坐标为（5，0）．

观察函数图象可知：当0＜x＜5时，一次函数y=﹣x+5的图象在第一象限，

∴当函数图象在第一象限时，自变量x的取值范围是0＜x＜5．

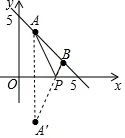
（3）作点A关于x轴的对称点A′，连接A′B交x轴于点P，此时点P为所求的点，如图所示．

∵点A（1，4），

∴A′（1，﹣4）．

设直线A′B的解析式为y=kx+b，

将A′（1，﹣4）、B（3，2）代入y=kx+b，

，解得：，

∴直线A′B的解析式为y=3x﹣7．

当y=3x﹣7=0时，x=，

∴点P的坐标为（，0）．

【点评】：

本题考查了待定系数法求一次函数解析式、一次函数图象上点的坐标特征以及轴对称中的最短路线问题，解题的关键是：（1）由点A的坐标利于待定系数法求出直线AB的解析式；（2）利于一次函数图象上点的坐标特征求出直线AB与x轴的交点坐标；（3）根据两点之间线段最短，找出点P的位置．

九

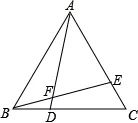
如图，△ABC是等边三角形，点D、E分别在BC、AC上，且BD=CE，AD与BE相交于点F．

（1）试说明△ABD≌△BCE；

（2）△EAF与△EBA相似吗？说说你的理由．

【答案】

【分析】：

（1）根据等边三角形各边长相等和各内角为60°的性质可以求证△ABD≌△BCE；

（2）根据全等三角形对应角相等性质可得∠BAD=∠CBE，进而可以求得∠EAF=∠EBA，即可求证△EAF∽△EBA，即可解题．

【解答】：

（1）证明：∵△ABC是等边三角形，

∴AB=BC，∠ABD=∠BCE=∠BAC，

又∵BD=CE，

∴△ABD≌△BCE；

（2）答：相似；

理由如下：

∵△ABD≌△BCE，

∴∠BAD=∠CBE，

∴∠BAC﹣∠BAD=∠CBA﹣∠CBE，

∴∠EAF=∠EBA，又∵∠AEF=∠BEA，

∴△EAF∽△EBA．