中考数学二次函数解析式专项练习题(含答案)
发布于 2021-09-03 14:05 ,所属分类:数学资料学习库



(2)设销售单价为每千克x元,月销售利润为y元,求y与x的函数表达式(不必写出x的取值范围);
(3)商店想在月销售成本不超过10000元的情况下,使得月销售利润达到8000元,销售单价应定为多 少?

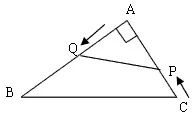

(2)设△FCQ的面积为y (cm2),求y与t之间的函数关系式;
(3)线段FQ能否经过线段AC的中点,若能,请求出此时t的值,若不能,请说明理由;
(4)设△FPQ的面积为S (cm2),求S与t之间的函数关系式,并回答,在t的取值范围内,S是如何随t的变化而变化的。

(2)求y与x之间的函数关系式;
(3)当每桶食用油的价格为55元时,可获得多少利润?
(4)当每桶食用油的价格定为多少时,该商店一天销售这种食用油获得的利润最大? 最大利润为多少?

(2)试求
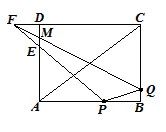
 MPA面积的最大值,并求此时x的值。
MPA面积的最大值,并求此时x的值。(3)请你探索:当x为何值时,
 MPA是一个等腰三角形?你发现了几种情况?写出你的研究成果。
MPA是一个等腰三角形?你发现了几种情况?写出你的研究成果。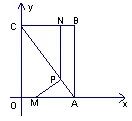

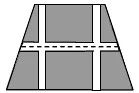
(2)当三条甬道的面积是梯形面积的八分之一时,求甬道的宽;
(3)根据设计的要求,甬道的宽不能超过6米,如果修建甬道的总费用(万元)与甬道的宽度成正比例关系,比例系数是5.7,花坛其余部分的绿化费用为每平方米0.02万元,那么当甬道的宽度为多少米时,所建花坛的总费用最少?最少费用是多少万元?

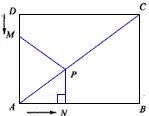
(2)试求△MPA的面积S与时间x秒的函数关系式,写出自变量x的取值范围,并求出S的最大值;
(3)在这个运动过程中,△MPA能否为一个等腰三角形.若能,求出所有x的对应值;若不能,请说明理由.


(2)根据上表,写出在第x周期后时,该细胞的总个数y(用x、n表示);
(3)当n=21时细胞在第几周期后时细胞的总个数最多?最多是多少个?

(2)8000元是否为每月销售这种篮球的最大利润?如果是,请说明理由;如果不是,请求出最大利润,此时篮球的售价应定为多少元?
◆◆答案解析◆◆
令10x2+90x=700,解得x=5,
答:前5个月的利润和等于700万元。
(2)令10x2+90x=120x,
解得x=3,
答:当x为3时,使用回收净化设备后的1至x月的利润和与不安装回收净化设备时x个月的利润和相等。
(3)使用回收净化设备后两年的利润总和为:12(10×12+90)+12(10×12+90)=5040(万元)。
(2)y=-10x2+1400x-40000;
(3)要使月销售利润达到8000元,即y=8000
所以-10x2+1400x-40000=8000
则x1=60,x2=80
当销售单价定为每千克60元时,月销售量为500-(60-50)×10=400(千克),月销售成本为40×400=16000(元)
当销售单价定为每千克80元时,月销售量为500(80-20)×10=200(千克),月销售成本为40×200=8000(元)
由于8000<10000<16000
而且销售成本不能超过10000元,所以销售单价应定为每千克80元。
2.设△APQ的面积为S,
(1)△APQ的面积S与t的关系式为:S=
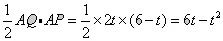 即S=6t-t2
即S=6t-t2(2)当t=2s时,△APQ的面积S=6×2-22=8(cm2)
3.当t为多少秒时,以点A、P、Q为顶点的三角形与△ABC相似
(1)当
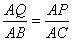 时
时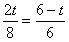 ∴t=2.4(s)
∴t=2.4(s)(2)当
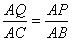 时,
时,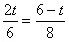 ∴
∴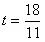
综上所述,当t为2.4秒或
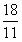 时,以点A、P、Q为顶点的三角形与△ABC相似。
时,以点A、P、Q为顶点的三角形与△ABC相似。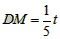
(2) S△FCQ=5t
(3)
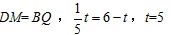
(4)
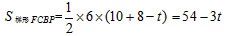
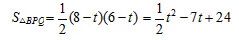
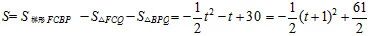
S随t的增大而减小。
即:从t=0,S=30变化到 t=6,S=6
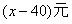 ,
,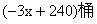 或
或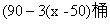 ;
;由题意
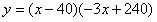
整理得
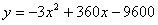
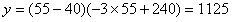
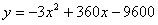
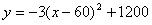
则:当x=60时,y的最大值为1200
答:当每桶食用油的价格定为60元时,该商店每天销售这种食用油获得的利润最大。
最大利润为1200元。
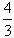 x );
x );(2)设
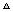 MPA的面积为S,在
MPA的面积为S,在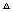 MPA中,MA=6-x,MA边上的高为
MPA中,MA=6-x,MA边上的高为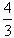 x,
x,其中,0≤x≤6
∴S=
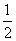 (6-x)×
(6-x)×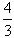 x=
x=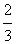 (-x2+6x) = -
(-x2+6x) = -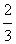 (x-3)2+6
(x-3)2+6∴S的最大值为6, 此时x =3;
(3)延长NP交x轴于Q,则有PQ⊥OA
①若MP=PA ∵PQ⊥MA ∴MQ=QA=x. ∴3x=6, ∴x=2;
②若MP=MA,则MQ=6-2x,PQ=
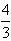 x,PM=MA=6-x
x,PM=MA=6-x在Rt
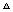 PMQ中,∵PM2=MQ2+PQ2
PMQ中,∵PM2=MQ2+PQ2∴(6-x)2=(6-2x)2+ (
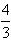 x)2∴x=
x)2∴x=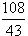
③若PA=AM,∵PA=
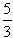 x,AM=6-x ∴
x,AM=6-x ∴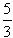 x=6-x ∴x=
x=6-x ∴x=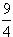
综上所述,x=2,或x=
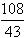 ,或x=
,或x=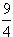 。
。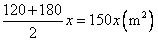
(2)依题意:
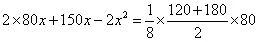
整理得:
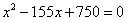
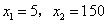 (不符合题意,舍去)
(不符合题意,舍去)∴甬道的宽为5米.
(3)设建设花坛的总费用为y万元.
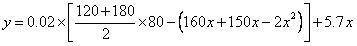
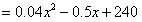
当
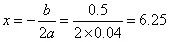 时,y的值最小.
时,y的值最小.因为根据设计的要求,甬道的宽不能超过6米,
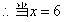 米时,总费用最少.
米时,总费用最少.最少费用为:
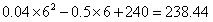 万元
万元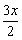 .
.(2)过点P作PQ⊥AD交AD于点Q. 可知PQ=AN=2x.
依题意,可得AM=3-x.
∴S=
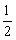 ·AM·PQ=
·AM·PQ=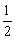 ·(3-x)·2x=-x2+3x=-
·(3-x)·2x=-x2+3x=- .
.自变量x的取值范围是:0<x≤2.
∴当x=
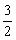 时,S有最大值,S最大值=
时,S有最大值,S最大值=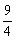 .
.(3)△MPA能成为等腰三角形,共有三种情况,以下分类说明:
①若PM=PA, ∵PQ⊥AD,∴MQ=QA=PN=
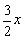 .
.又DM+MQ+QA=AD ∴4x=3,即x=
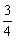 .
.②若MP=AM, MQ=AD-AQ-DM=3-
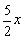 ,PQ=2x,MP=MA=3-x.
,PQ=2x,MP=MA=3-x.在Rt△PMQ中,由勾股定理得:MP2=MQ2+PQ2.
∴(3-x)2=(3-
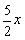 )2+(2x)2.
)2+(2x)2.解得x=
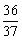 ,x=0(不合题意,舍去)
,x=0(不合题意,舍去)③若AP=AM, 由题意可求AP=
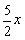 ,AM=3-x.
,AM=3-x.∴
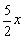 =3-x.解得x=
=3-x.解得x=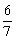 .
.综上所述,当x=
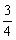 ,或x=
,或x=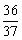 ,或x=
,或x=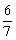 时,△MPA是等腰三角形.
时,△MPA是等腰三角形.5(n-4)-5+(n-5)=6(n-5);
(2)
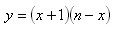 ;
;(3)当n=21时,
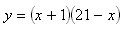 =
=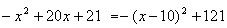
所以,当x=10时,
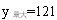 。
。(2)设月销售利润为W元,
由题意得
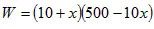
整理得
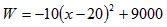
当x=20时,W有最大值9000,
而20+50=70,
答:8000元不是最大利润,最大利润为9000元,此时篮球的售价为70元。
推荐阅读:
初中数学就是这15张图+89个重要知识点
初中数学三大专题100道基础好题,一定要转给孩子好好练练!
初中数学相似三角形13大知识点6大常考经典例题解析
中考数学函数及图像知识点总结含典型例题
文章|网络,版权归原作者及原出处所有,侵删。

长按识别ErWeiMa更多精彩











![25篇高中英语语法填空专项训练(PDF文档含答案)[百度云资源]](https://static.kouhao8.com/cunchu/cunchu7/2023-05-18/UpFile/defaultuploadfile/230425ml/251-1.jpg?x-oss-process=image/format,webp/resize,w_88/crop,w_88,h_88,g_nw)



![高考英语:3500单词配套练习含答案 1-26课时 word文档[百度网盘资源]](https://static.kouhao8.com/cunchu/cunchu7/2023-05-18/UpFile/defaultuploadfile/230425ml/154-1.jpg?x-oss-process=image/format,webp/resize,w_88/crop,w_88,h_88,g_nw)
相关资源