初中数学|截长补短模型

【专题说明】

截长补短法在初中几何教学中有着十分重要的作用,它主要是用来证线段的和差问题,而且这种方法一直贯穿着整个几何教学的始终.那么什么是截长补短法呢?所谓截长补短其实包含两层意思,即截长和补短.截长就是在较长的线段上截取一段等于要证的两段较短的线段中的一段,证剩下的那一段等于另外一段较短的线段.当条件或结论中出现a+b=c时，用截长补短．

截长补短法常常与旋转相通。

【知识总结】

1、补短法：通过添加辅助线“构造”一条线段使其为求证中的两条线段之和，在证所构造的线段和求证中那一条线段相等；

2、截长法：通过添加辅助线，先在求证中长线段上截取与线段中的某一段相等的线段，在证明截剩部分与线段中的另一段相等。

3、截长法与补短法，具体做法是在某条线段上截取一条线段与特定线段相等，或是将某条线段延长，使之与特定线段相等，再利用三角形全等的有关性质加以说明，这种做法一般遇到证明三条线段之间关系是常用.

【经典例题】

【例1】【问题情境】

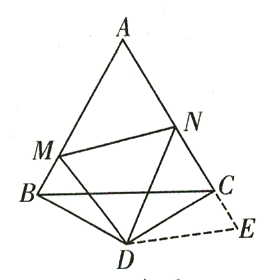
在等边△ABC的两边AB，AC上分别有两点M，N，点D为△ABC外一点，且∠MDN＝60°，∠BDC＝120°，BD＝DC．

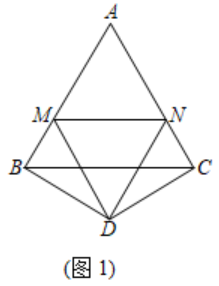
【特例探究】

如图1，当DM＝DN时，

（1）∠MDB＝（）度；

（2）MN与BM，NC之间的数量关系为（）；

【归纳证明】

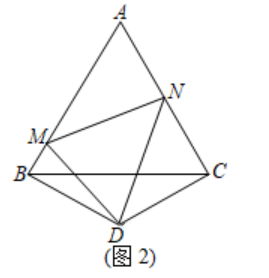
如图2，当DM≠DN时，猜想MN与BM，NC之间的数量关系，并加以证明．

【拓展应用】

△AMN的周长与△ABC的周长的比为（）．

【分析】【特例探究】（1）先证明△MDN是等边三角形，则MN＝DM＝DN，再证明Rt△DBM≌Rt△DCN（HL），得∠BDM＝∠CDN＝30°；

（2）由（1）得DM＝2BM，可得结论MN＝2BM=BM+NC；

【归纳证明】先证△DBM≌△DCE（HL），得DM＝DE，∠BDM＝∠CDE，再证△MDN≌△EDN（SAS），得MN＝NE，可得结论MN＝BM+CN；

【拓展应用】由（1）（2）得：MN＝BM+NC，则△AMN的周长＝2AB，△ABC的周长＝3AB，即可得出结论．

【解答】【特例探究】

解：（1）∵DM＝DN，∠MDN＝60°，

∴△MDN是等边三角形，

∴MN＝DM＝DN，∵∠BDC＝120°，BD＝DC，

∴∠DBC＝∠DCB＝30°，

∵△ABC是等边三角形，

∴∠ABC＝∠ACB＝60°，

∴∠DBM＝∠DCN＝90°，

∵BD＝CD，DM＝DN，

∴Rt△DBM≌Rt△DCN（HL），

∴∠MDB＝∠NDC＝30°，

故答案为：30；

（2）由（1）得：DM＝2BM，DM＝MN，Rt△DBM≌Rt△DCN（HL），

∴BM＝CN，

∴DM＝MN＝2BM＝BM+NC，

即MN＝BM+NC；

【归纳证明】

解：猜想：MN＝BM+NC，证明如下：

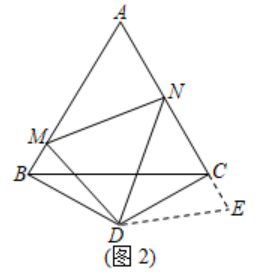
如图，延长NC到点E，使CE＝BM，连接DE，

∵△ABC是等边三角形，

∴∠ABC＝∠ACB＝60°，

∵BD＝CD，∠BDC＝120°，

∴∠DBC＝∠DCB＝30°，

∴∠MBD＝∠NCD＝90°．

∴∠MBD＝∠ECD＝90°，

又∵BD＝CD，BM＝CE，

∴△DBM≌△DCE（SAS），

∴DM＝DE，∠MDB＝∠EDC，

∵∠MDN＝60°，∠BDC＝120°，

∴∠MDB+∠NDC＝60°，

∴∠EDN＝∠NDC+∠EDC＝∠MDB+∠NDC＝60°，

∴∠EDN＝∠MDN，

又∵DN＝DN，

∴△MDN≌△EDN（SAS），

∴MN＝EN＝EC+NC＝BM+NC；

【点评】此题是三角形的综合题，考查了等边三角形的判定与性质，含30°角的直角三角形，等腰三角形的性质以及全等三角形的判定与性质等知识．此题综合性很强，熟练掌握等边三角形的判定与性质，证明三角形全等是解题的关键，属于中考常考题型．

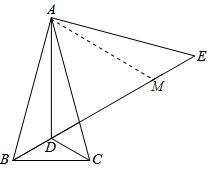
【例2】如图，在△ABC中，AB＝AC，∠BAC＝30°，点D是△ABC内一点，DB＝DC，∠DCB＝30°，点E是BD延长线上一点，AE＝AB．

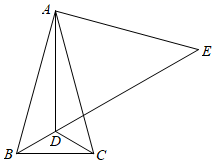
（1）求∠ADB的度数；

（2）线段DE，AD，DC之间有什么数量关系？请说明理由．

【分析】

（1）根据三角形内角和定理得到∠ABC＝∠ACB＝75°，根据全等三角形的性质得到∠BAD＝∠CAD＝15°，根据三角形的外角性质计算，得到答案；

（2）在线段DE上截取DM＝AD，连接AM，得到△ADM是等边三角形，根据△ABD≌△AEM，得到BD＝ME，结合图形证明结论

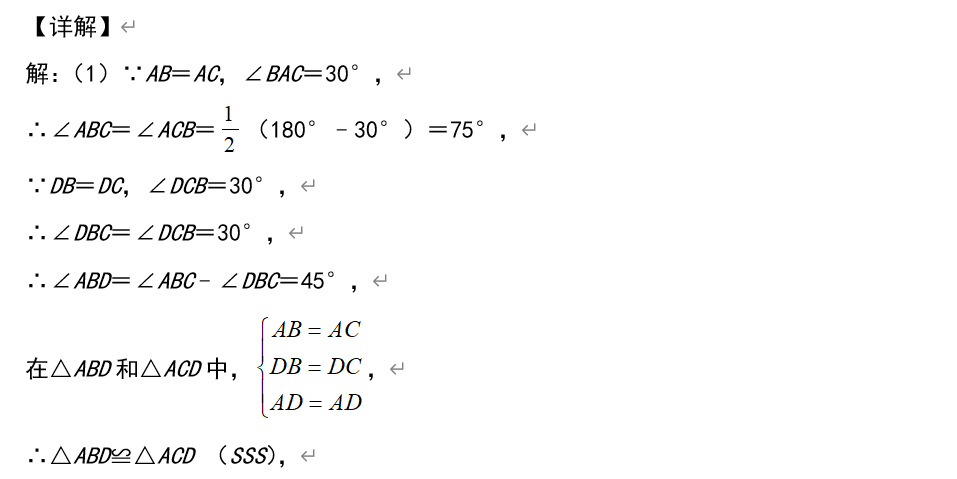
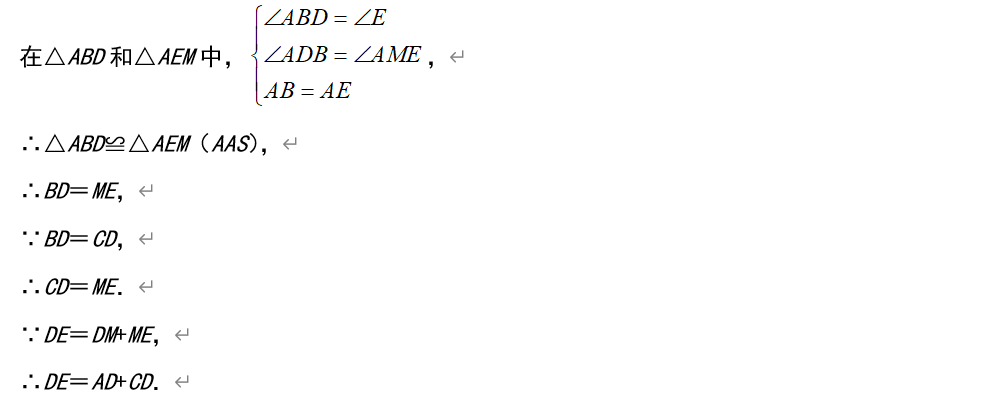
【点睛】

本题考查的是全等三角形的判定和性质、等边三角形的判定和性质，掌握全等三角形的判定定理和性质定理是解题的关键．

【巩固】如图，△ABC是边长为2的等边三角形，△BDC是顶角为120°的等腰三角形，以点D为顶点作∠MDN=60°，点M、N分别在AB、AC上．

（1）如图①，当MN//BC时，则△AMN的周长为______；

（2）如图②，求证：BM+NC=MN．

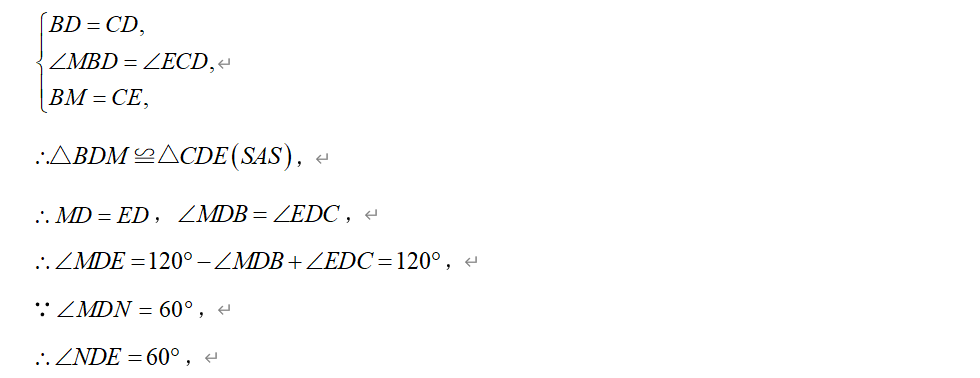
【点睛】

本题考查了全等三角形的判定与性质及等边三角形的性质及等腰三角形的性质，掌握全等三角形的性质与判定，等边三角形及等腰三角形的性质是解题的关键．