深度学习数学基础

深度学习是什么？深度的学习，不断挖掘，这是字面的理解，深度学习是机器学习的一个分支，主要是通过模拟人脑神经网络系统的运作模式，达成人工智能的效果。北大生命科学学院院长尧毅先生在一次讲座中认为是伪科学，他认为人脑神经科学才是真科学。学科领域之间的通融才是科学技术发展的“康庄大道”。

听过了常州吴老师关于人工智能算法应用的讲座，略看过人工智能的实战操演。“神奇”是关键词。背后到底是什么在发挥关键作用，今天聊聊我眼中的深度学习数学基础。

一、深度学习中神经网络的基本思想

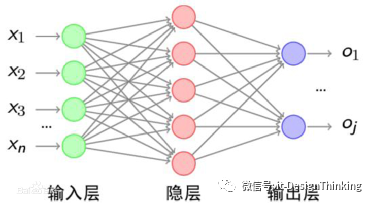
举例，我们将一个图像的各个像素信息作为输入，即为X_i，隐层完成模式的识别，即特征值的匹配，最后产生结果O₁~O_j 。但是作为独立的神经元个性而言，最终的结果只有两种，0与1，这是图是猫吗？是还是不是？还有一种可能，这个图好像是只猫，像的比率是多少？——哈哈，这就是概率，也就是经典计算机算法是以数论、组合数学为基础的，现代算法是以概率论与统计学为基础。YES，时代进步了。

二、神经单元的数学表达

我们来看一下单个的神经元单元

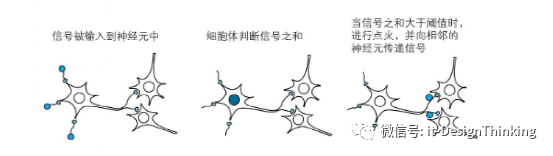
所以，假设神经元输出为 y，固定值为 θ，输入信号的权值和输入信号的强度为wn 和xn

可得到如下表达式：

w1*x1 + w2*x2 + ... wn*xn < θ => y=0

w1*x1 + w2*x2 + ... wn*xn > θ => y=1

数学上有一个 单位阶跃函数的定义，自变量大于0时，函数值为1；自变量小于0时，函数值为0，自变量为0时函数值为不确定或不定义。

数学中能找出一个表达阶跃函数，并且连续还处处可导，还计算方便的激发函数来模拟神经单元？你别说，还真有，Sigmoid函数。

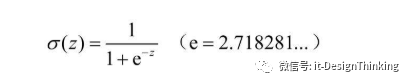
它有神奇的特点，第一点：处处可导，为什么要处处可导，人工智能的本质就是给一堆数据，我们要找出原本的F(x,y,z....)关系。怎么找？我们可以让误差变小，慢慢，逐步趋近最优解。误差如果最小。最小二乘法，1829年，高斯提供了最小二乘法的优化效果强于其他方法的证明。最小二乘法的基础就是抛物线最值问题,可扩展到N元。

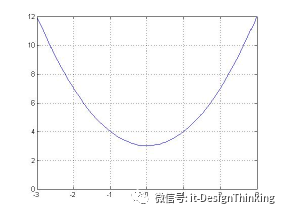
第二点神奇的地方：σ（Z）的导数=σ（Z）（1-σ（Z）），也就是它本身的导数只要做基本运算即可。

三、误差反向传播的链式法则

我们目标是要估计出原始的关系，如下例子。

计算图将计算过程用图形来表示。这里说的图形是数据结构图，通过多个节点和边表示（连接节点的直线称为“边”）。下面用一个实例来说明：

例，昆山兵希超市里苹果每个100元，消费税是 10%。如果买 2 个苹果，请计算支付金额。

计算图如下：

如上图所示，开始时，苹果的单价100元和苹果的个数2一起流到“×”节点，变成200元，然后被传递给下一个节点。接着，这个200元和消费税1.1一起流向第二个“×”节点，变成220元。因此，从这个计算图的结果可知，答案为220元。

用计算图解题的情况下，需要按如下流程进行：

1）构建计算图

2）在计算图上，从左向右进行计算

这里的第 2 歩“从左向右进行计算”是一种正方向上的传播，简称为正向传播（forward propagation）。正向传播是从计算图出发点到结束点的传播。考虑反向（从图上看的话，就是从右向左）的传播。实际上，这种传播称为反向传播（backward propagation）。反向传播将在接下来的导数计算中发挥重要作用。

假设我们想知道苹果价格的上涨会在多大程度上影响最终的支付金额，即求“支付金额关于苹果的价格的导数”。设苹果的价格为x，支付金额为y，则相当于求y对于x的导数（物理当中就是加速度，经济学中是边际效益）。这个导数的值表示当苹果的价格稍微上涨时，支付金额会增加多少。

“支付金额关于苹果的价格的导数”的值可以通过计算图的反向传播求出来。结果如下图所示：

如图所示，反向传播使用与正方向相反的箭头（粗线）表示。反向传播传递“局部导数”，将导数的值写在箭头的下方。在这个例子中，反向传播从右向左传递导数的值（1 → 1.1 → 2.2）。从这个结果中可知，“支付金额关于苹果的价格的导数”的值是2.2。这意味着，如果苹果的价格上涨1日元，最终的支付金额会增加2.2日元（严格地讲，如果苹果的价格增加某个微小值，则最终的支付金额将增加那个微小值的2.2倍）。

这里只求了关于苹果的价格的导数，不过“支付金额关于消费税的导数”、“支付金额关于苹果的个数的导数”等也都可以用同样的方式算出来。并且，计算中途求得的导数的结果（中间传递的导数）可以被共享，从而可以高效地计算多个导数。综上，计算图的优点是，可以通过正向传播和反向传播高效地计算各个变量的导数值。

四、梯度下降法的含义

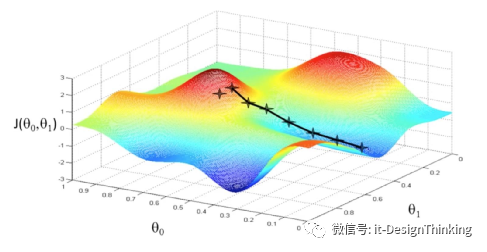
梯度下降法的基本思想可以类比为一个下山的过程。

假设这样一个场景：一个人被困在山上，需要从山上下来(找到山的最低点，也就是山谷)。但此时山上的浓雾很大，导致可视度很低；因此，下山的路径就无法确定，必须利用自己周围的信息一步一步地找到下山的路。这个时候，便可利用梯度下降算法来帮助自己下山。怎么做呢，首先以他当前的所处的位置为基准，寻找这个位置最陡峭的地方，然后朝着下降方向走一步，然后又继续以当前位置为基准，再找最陡峭的地方，再走直到最后到达最低处，为什么要到最低处？找出函数的最小值，也就是误差最小，也就是越来越接近原函数。机器学习的本质不就是此麻。这部分要用到偏导，为什么？三维空间或多维空间，我们只有视其它为常量，求单因子导数，偏导就在这个地方起到了关键作用。当导数为0，不就可能是最小值。

综上所述，人工智能是以微积为为基础，概率统计为核心，迭代收敛为目标路径的一套算法体系。这才是深度学习的根基与本质。