【每日一题】初中(7-9年级)数学培优提升(第37期答案)

发布于 2021-09-03 14:12 ，所属分类：数学资料学习库

gongzhong号，可在微信好友里自动收到每天的推送，还可以查看全部资源。

识别下面ErWeiMagongzhong号

七、八、九年级的童鞋们，每天都可以从这拿到一道数学题哦！知识强化、课外拓展、思维提升，都在这一道数学题里了。
提醒大家：题目不简单，够胆来挑战！请认真答题，一定要坚持住哦！也欢迎邀请同学参与到我们的答题中哦！
刷屏到文末，点击左下角“”可查看“7-9年级”全部课程。

第37期答案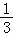


七

4a2+2a3﹣ab2c+25是　 　次　 　项式，最高次项是　 　，最高次项的系数是　 　，常数项是　 　．



【答案】

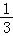四，四，﹣ab2c，﹣，25


【解答】：

4a2+2a3﹣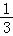ab2c+25是四次四项式，最高次项是﹣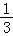ab2c，最高次项的系数是﹣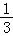，常数项是25．

故答案为四，四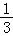，﹣ab2c，﹣，25．


【点评】：本题考查了多项式的有关定义．

解答此题的关键是熟知以下概念：

几个单项式的和叫做多项式，其中每个单项式叫做多项式的项；

一个多项式含有几项，是几次，就叫做几次几项式；

多项式里次数最高的项，叫作这个多项式的最高次项；

多项式里次数最高次项的数字因数叫做这个多项式最高项的系数；

多项式中不含字母的项叫常数项．


八

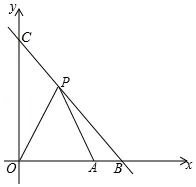
如图，直线y=﹣x+10与x轴、y轴分别交于点B，C，点A的坐标为（8，0），P（x，y）是直线y=﹣x+10在第一象限内一个动点．


（1）求△OPA的面积S与x的函数关系式，并写出自变量的x的取值范围；

（2）当△OPA的面积为10时，求点P的坐标．


【答案】

【分析】

【点评】：

本题考查了一次函数图象上点的坐标特征和一次函数的性质，把求三角形的面积和一次函数的图象结合起来，综合性比较强．


九

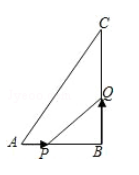
在△ABC中，∠B=90°，AB=6cm，BC=12cm，点P从点A开始沿AB边向点B以1cm/s的速度移动，点Q从点B开始沿BC边向点C以2cm/s的速度移动，设P、Q两点同时出发，移动时间为t秒．


（1）几秒钟后△PBQ是等腰三角形？

（2）几秒钟后△PQB的面积为5cm2？

（3）几秒钟后，以P、B、Q为顶点的三角形和△ABC相似？



【答案】

【分析】：

分别写出BP、BQ的关系式，

（1）△PBQ是等腰三角形，则根据BP=BQ即可求得t的大小，即可解题；

（2）写出△PQB的面积的表达式，根据BQ、BP的关系式和面积为10cm2即可求得t的大小，即可解题

（3）要使得△BPQ∽△BAC，则使得=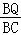即可．


【解答】：


——END——


来源：本文内容来源于网络，我们尊重原创，如有侵权联系删除。
点击左下角“”可查看“7-9年级”全部课程。

相关资源