普林斯顿博士数学教学方法 跟儿子一起阅读批判七年级数学上册

作者：乐乐 & 自然

本文分为两个部分：前边的主体部分是给课本提建议，提供好的学习方法；后边的补充部分是表扬课本中的正能量，以及批评家委会和学校老师策划出的“学习策略”。慢慢读，定有收获。

牛顿：柏拉图是我的朋友，亚里士多德是我的朋友，但我最重要的朋友是真理。

Plato is my friend, Aristotle is my friend, but my greatest friend is truth.

丘成桐：他（普林斯顿大学的布劳迪博士）有一套独特的教学法，他找来一本高深的数学著作，然后要求学生在书中找错误，并提出改正方法，这是让我们不要盲目依赖书本的良方，同时也训练了我对书本上的定理采取存疑的态度。（丘成桐：《培养崇高理想抱定赤子之心》）

丘成桐：......当你在一门课里面，基本功夫搞得很清楚以后，你就发现书里面很多是错的。在发现书本里的错误时，你的基本功夫也不错了。（丘成桐：我研究数学的经验）

“做数学就像是和女孩子睡，”老大哥如此说，“第一次或许有点儿麻烦，但下一次就会顺利得多了。”（丘成桐：《我的几何人生》）

课本说，几何是研究“形”的学问，这种说法太肤浅，正如徐光启所言，几何乃数之根本。

徐光启：《几何原本》者，度数之宗，所以穷方圆平直之情，尽规矩准绳之用也......（《徐光启：刻〈几何原本〉序》）

在徐光启看来，几何是“多少”、“几多”的意思。

陈省身：...几何是很重要的，因为大家觉得几何就是数学。比方说，现在还有这一印象，法国的科学院，它的数学组叫做几何组。对于法国来讲，搞数学的不称数学家，而叫几何学家...（陈省身：什么是几何学）

其实几何研究的是量，它研究的是各种东西之间的数量关系，这个我们从一开篇就提出的量与量之间关系的五大公理贯通了《原本》中（《原本》全书涵盖平面图形、代数、比例论、数论、无理量和体积）所有命题这一事实就能看出。

▲海豚也懂数量 —— Human Universe

华罗庚：数（读作shù）起源于数（读作Shǔ），如一、二、三、四、五……，一个、两个、三个…….量（读作liàng）起源于量（读作liáng）。先取一个单位作标准，然后一个单位一个单位地量。天下虽有各种不同的量(各种不同的量的单位如尺、斤、斗、秒、伏特、欧姆和卡路里等等)，但都必须通过数才能确切地把实际的情况表达出来。所以“数”是各种各样不同量的共性，必须通过它才能比较量的多寡，才能说明量的变化。（华罗庚：《华罗庚科普著作选集》）

华罗庚所说的第一个“数（读作shù）”是名词，第二个“数（读作Shǔ）”是动词，意思是：用“数（读作Shǔ）”这种行动方式才能建立“数（读作shù）”这个概念。

华罗庚所说的第一个“量（读作liàng）”是名词，第二个“量（读作liáng）”是动词，意思是：用“量（读作liáng）”这种行动方式才能建立“量（读作liàng）”这个概念。

罗素（1872年～1970年）：几何学对于哲学与科学方法的影响一直是深远的。希腊人所建立的几何学是从自明的、或者被认为是自明的公理出发，根据演绎的推理前进,而达到那些远不是自明的定理。公理和定理被认为对于实际空间是真确的,而实际空间又是经验中所有的东西。这样，首先注意到自明的东西然后再运用演绎法，就好像是可能发现实际世界中一切事物了。这种观点影响了柏拉图和康德以及他们两人之间的大部分的哲学家。“独立宣言”说：“我们认为这些真理是自明的”，其本身便脱胎于欧几里得。十八世纪天赋人权的学说，就是一种在政治方面追求欧几里德式的公理。牛顿的《原理》一书，尽管它的材料公认是经验的,但是它的形式却完全是被欧几里德所支配着的。（罗素：《西方哲学史》 何兆武、李约瑟 译）

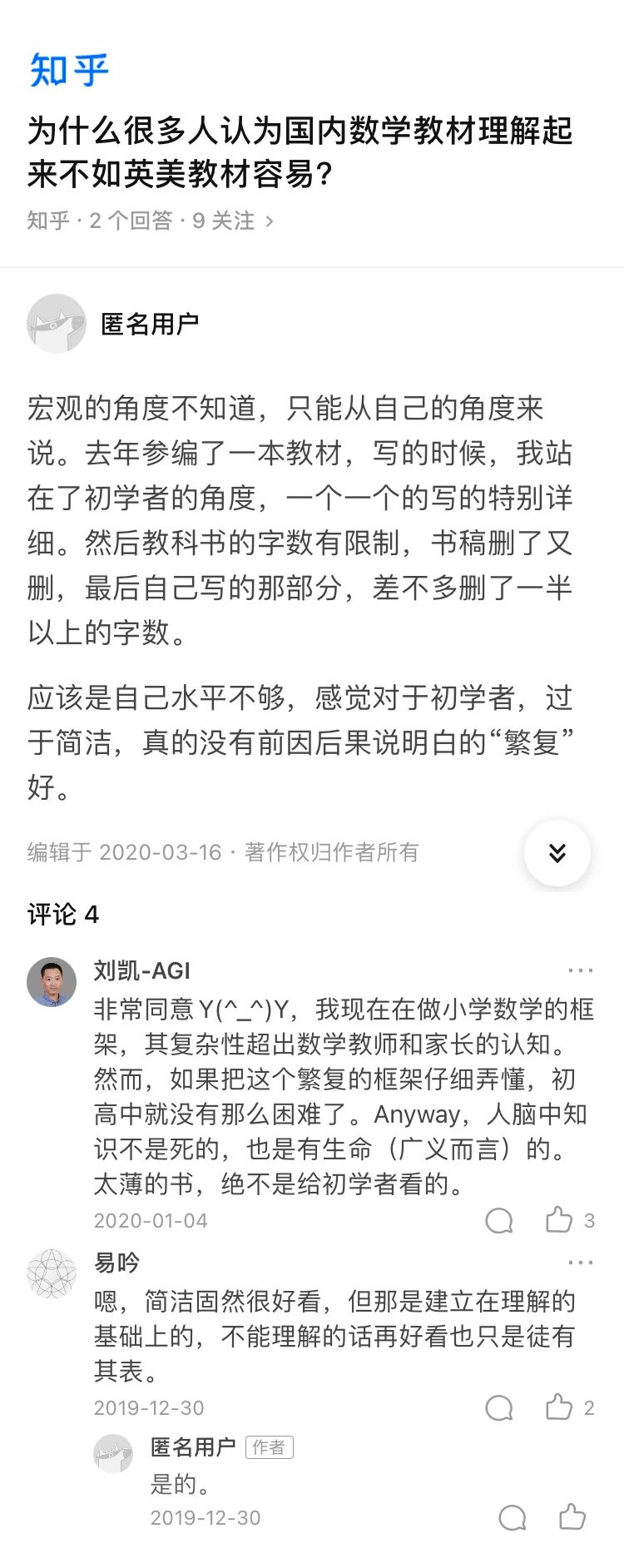
公理4：彼此重合的东西彼此相等。

Common notion 4：Things which coincide with one another are equal to one another.（The Thirteen Books of Euclid's Elements.by Euclid(Author), T.L.Heath(Translator)）

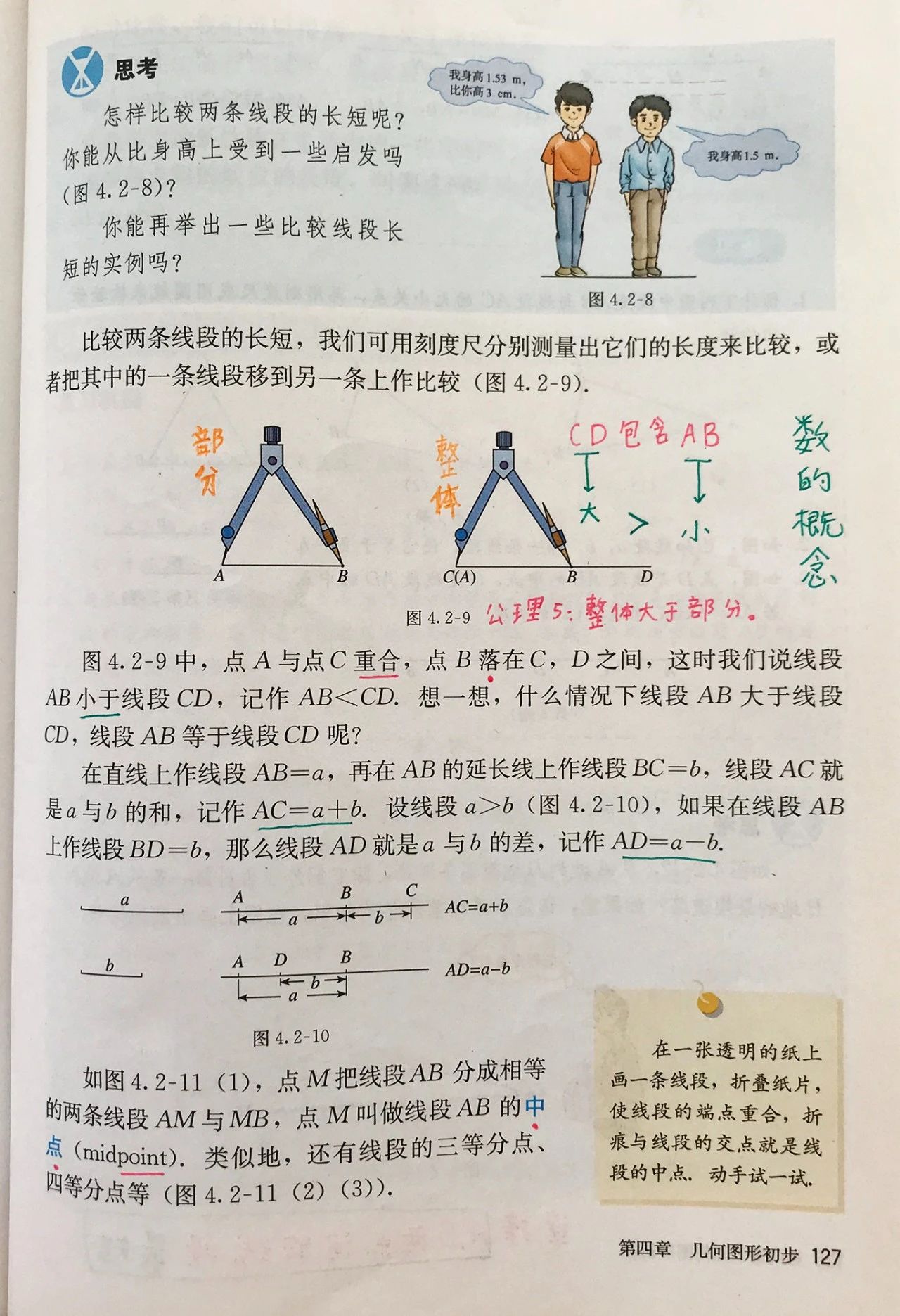
公理5：整体大于部分。

Common notion 5：The whole is greater than the part.（The Thirteen Books of Euclid's Elements.by Euclid(Author), T.L.Heath(Translator)）

欧几里得是在前人的基础之上总结出了贯穿图形关系的五大公设及融通数学逻辑的五大公理。这样的知识精华，这么伟大的总结，为什么课本不写出来告诉学生呢？难道是让学生自己把公理悟出来？

并不是每个人都能像欧几里得那般有时间和实力把公设和公理自己重新研究和构建出来。

牛顿：几何学的荣耀在于，用如此少的原理，就能获得如此众多的成就。

Isaac Newton：And geometry can boast that with so few principles obtained from other fields, it can do so much.【The Principia : Mathematical Principles of Natural Philosophy. by Isaac Newton (Author), I. Bernard Cohen (Translator), Anne Whitman (Translator),Julia Budenz (Translator)】

例3中的推理是咋回事？为什么两个东西合在一起的一半，等于这两个东西各自的一半的和？

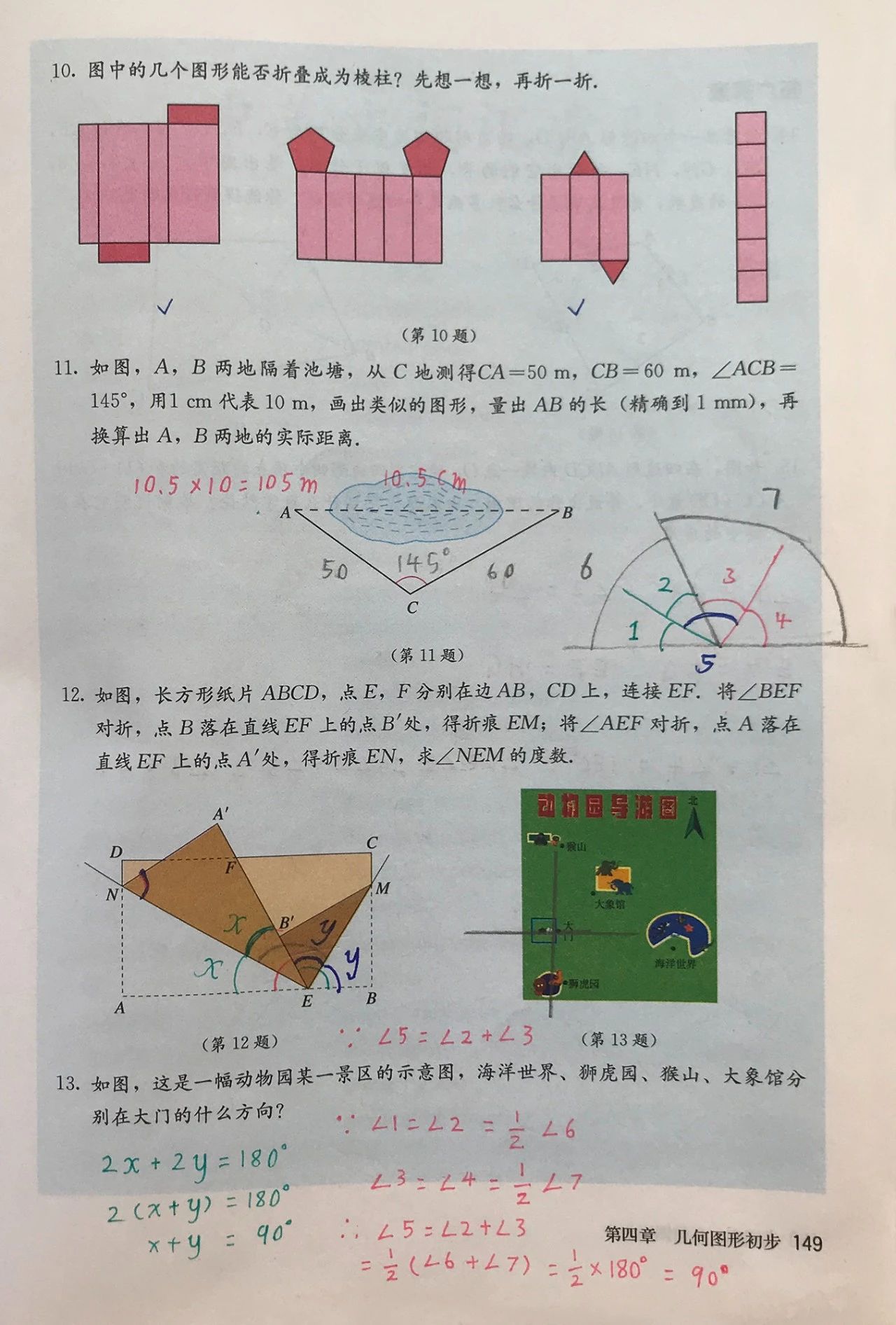
149页的第12题，只是137页中的例3换了一副马甲，为什么两个合在一起的东西的一半，等于这两个东西各自一半的和？为什么？

没有证明过的东西到处乱用，一点都不严谨。

这个定理的证明过程在《原本·第五卷·命题1》中，课本为什么不做补充说明或加以提示？

▲ The Thirteen Books of Euclid's Elements.by Euclid(Author), T.L.Heath(Translator)

在鸡兔同笼的问题中，古人也应用了这个定理（乘法分配律）。自然创意设计之前的文章《从鸡兔同笼看〈孙子算经〉与〈几何原本〉中，及南北朝人与古希腊人》对此定理的论证已详细阐述过了，这里不再赘述。

诺伯特·维纳：我开始认字看书的年龄，还不到其他许多儿童牙牙学语年龄的两倍，后来在父母的指导下，我学完了初级教科书......有两件使我感到困难的东西，也正是一个问题的两个对立面，即准确快速的加法、乘法运算技巧，以及对各种算术定律的了解，如交换律、结合律、分配律为什么是正确的。一方面我对课题的理解速度快，而运算跟不上；另一方面，我所需要知道的对一些基本的性质的解释，远远超过专门介绍运算的课本上的解释。（诺伯特·维纳：《昔日神童》）

课本说：“用算术的方法列式解题，算术的列式中只含有已知数；而方程中既含有已知数，又含有未知数。”

课本定义方程的方式是错误的，因为算术的列式中也是含有未知数的。

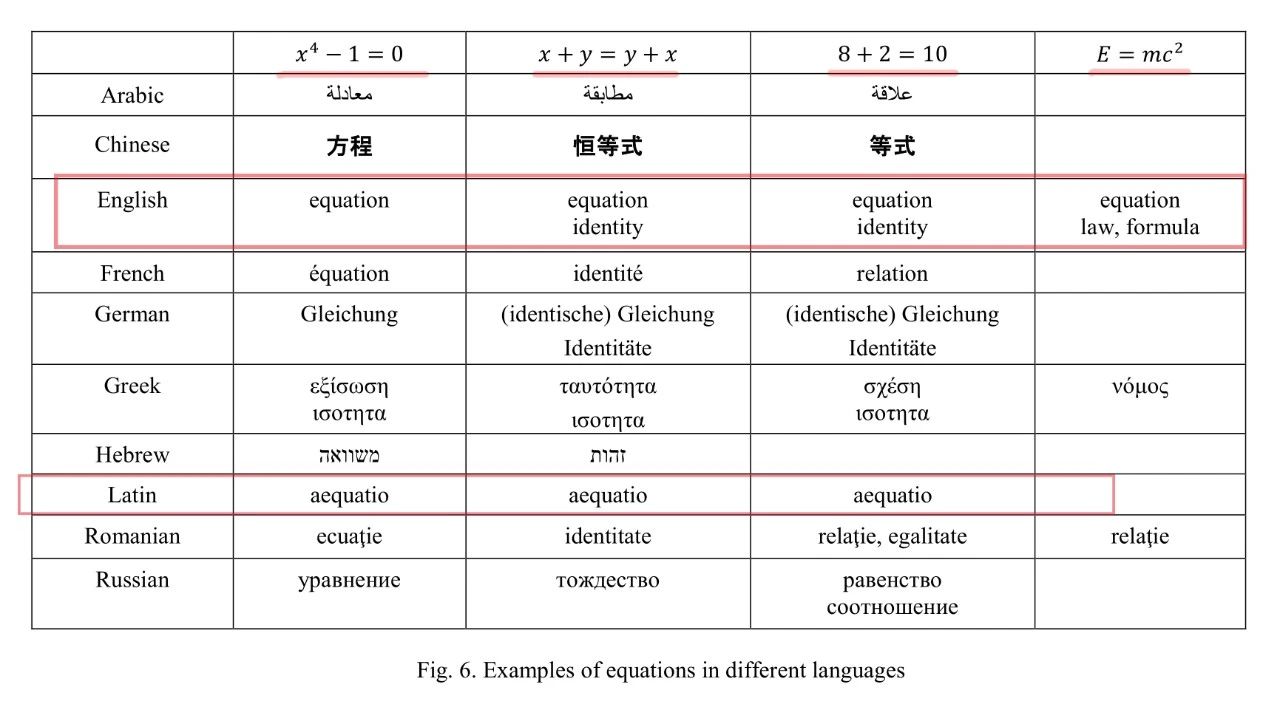
▲What is an Equation?

in English any equality is an equation.（What is an Equation? by Solomon Marcus, Stephen M. Watt）

课本所列的方程是这样的：X/60 - X/70 = 1

通过推导，我们可以把课本所列的这个方程转化为算术的列式：

X/60 - X/70 = 1

↓

X（1/60 - 1/70） = 1

↓

1/60 - 1/70 = 1 ÷ X

↓

1 ÷ （1/60 - 1/70） = X

↓

1 ÷ （1/60 - 1/70） = 420 （公里）

看，这个转化出来的算式，其实算式也是有未知数的，只不过算式的未知数被放在了等于号的后边。

所以，课本说的“用算术的方法列式解题，算术的列式中只含有已知数；而方程中既含有已知数，又含有未知数。”是错误的。因为算术的列式中也是有未知数的。

可能很多人都会觉得，在方程列式X/60 - X/70 = 1中，整个式子的逻辑顺序和意义都是明确的，是可以解释的，就是慢车跑完总路程的时间比快车跑完总路程的时间要多出了一个小时。

可能很多人都不清楚从方程X/60 - X/70 = 1转化过来的这个方程1 ÷ （1/60 - 1/70） = X 的内在逻辑顺序和意义是什么，因为作业帮之类的app上没有做这样的分析。

1 ÷ （1/60 - 1/70） = X 的内在逻辑非常有意思，我们用小数的形式，以及计算所得的近似值协助一下，就能解释清楚了：

1/60 - 1/70的意思是，将每一小时均分在60公里上，减去将每一小时均分在70公里上；意思是慢车在每1公里上所花费的时间都要比快车在每1公里上所花费的时间都多一些；那到底多多少呢？

1/60 - 1/70 ≈ 0.01667 - 0.01429 ≈ 0.00238（小时）

多大约0.00238小时。

重复一遍，慢车在每1公里上所花费的时间都要比快车在每1公里上所花费的时间多大约0.00238小时。

也就是说，慢车每多花一个0.0238小时这样的单位，从A地到B地就存在着一个1公里，时间与路程是对应的关系；其实就是一种等量代换（《原本》中的公理又出现了）的关系，每多出一个0.0238小时，就相当于存在一个1公里。如果不容易理解的话，还可以这样想，整体的运动过程是这样的：因为慢车每多花0.0238小时，快车都会走出1公里，所以0.0238小时是等价于1公里的。

题目告诉我们，慢车会晚点很多个（多花费很多个）这样的0.0238小时，慢车会晚点1个小时才能到达B地，即将这些晚了的0.0238小时全部都加起来的总和是1个小时。

反过来讲，总共晚点的这1个小时里有多少个0.0238存在，就有多少个1公里存在：

1 ÷ 0.00238 ≈ 420.2（公里）

1小时中大约有420.2个0.00238小时，即慢车大约晚点了（多花费了）420个0.0238小时，

每晚点（多花费）一个0.0238小时就会有一个1公里存在，所以从A地到B地的路程是420.2（公里）。

看，1 ÷ （1/60 - 1/70） = X 的内在逻辑顺序和意义，被解释清楚了。

所以，如果按课本给方程所下的定义(“方程中既含有已知数，又含有未知数”）来规定方程，只要是等式都可被看作方程。

只不过，大家在主观上认为他们所谓的方程，往往都是思路清晰的、容易让人明白的、不动脑子也能学得会的形式，跟套公式一样，解起题来特别容易。

而让大家头疼的算式当中的思路，往往都是一些稀奇古怪难以理解的东西，分析起来特别的费力和曲折，都是一些不动脑子很难学得会的东西。

除以上外，我们还可以用列出的其他方程及方程转化后的算式来证明算式也是方程，算式中的思路也是可以用逻辑解释清楚的。

我们设慢车和快车的行驶时间为X小时，可得出方程：

70X = 60X + 60

70X - 60X = 60

X = 6（小时）

进而得出从A地到B地的路程是：70X = 70 x 6 = 420 （公里）

然后我们也可以把这个方程改造成算式形式的方程：

70X = 60X + 60 （公里）

↓

（70 - 60）X= 60

↓

60 ÷（70 - 60）= X

前边这个60的意思是：慢车要晚1小时，即相当于慢车落后60公里

60【慢车比快车落后了60公里】÷（70 - 60）【快车每走70公里，就会比慢车多走出10公里。

60公里 ÷ 10 = 6（小时）【意思是，慢车总共落后的60公里当中有6个10公里，每一个10公里就相当于1小时，即慢车落后的60公里路程总共花费了6个小时，即慢车与快车都行走了6个小时】

同样，我们又得出了从A地到B地的路程是：70 x 6 = 420 （公里）【意思是：用行驶时间乘以快车的速度，得到的就是从A到B的距离420 公里】

↓

当然，我们也可以将60 ÷（70 - 60）= X与70 x 6 =420合并成一个算式：

60 ÷（70 - 60） x 70 = X

↓

60 ÷（70 - 60） x 70 = 420 （公里）

自然创意设计之前的文章《死记硬背数学公式，会形成思维障碍，公式会被颠覆公式不是万能的》中有更多关于路程、时间及速度的阐述，有兴趣者可点击阅读。

牛顿：能测量时间的匀速运动很可能是不存在的。所有的运动可能都是加速的或减速的...

Isaac Newton：It is possible that there is no uniform motion by which time may have an exact measure.All motions can be accelerated and retarded, but the flow of absolute time cannot be changed.【The Principia : Mathematical Principles of Natural Philosophy. by Isaac Newton (Author), I. Bernard Cohen (Translator), Anne Whitman (Translator),Julia Budenz (Translator)】

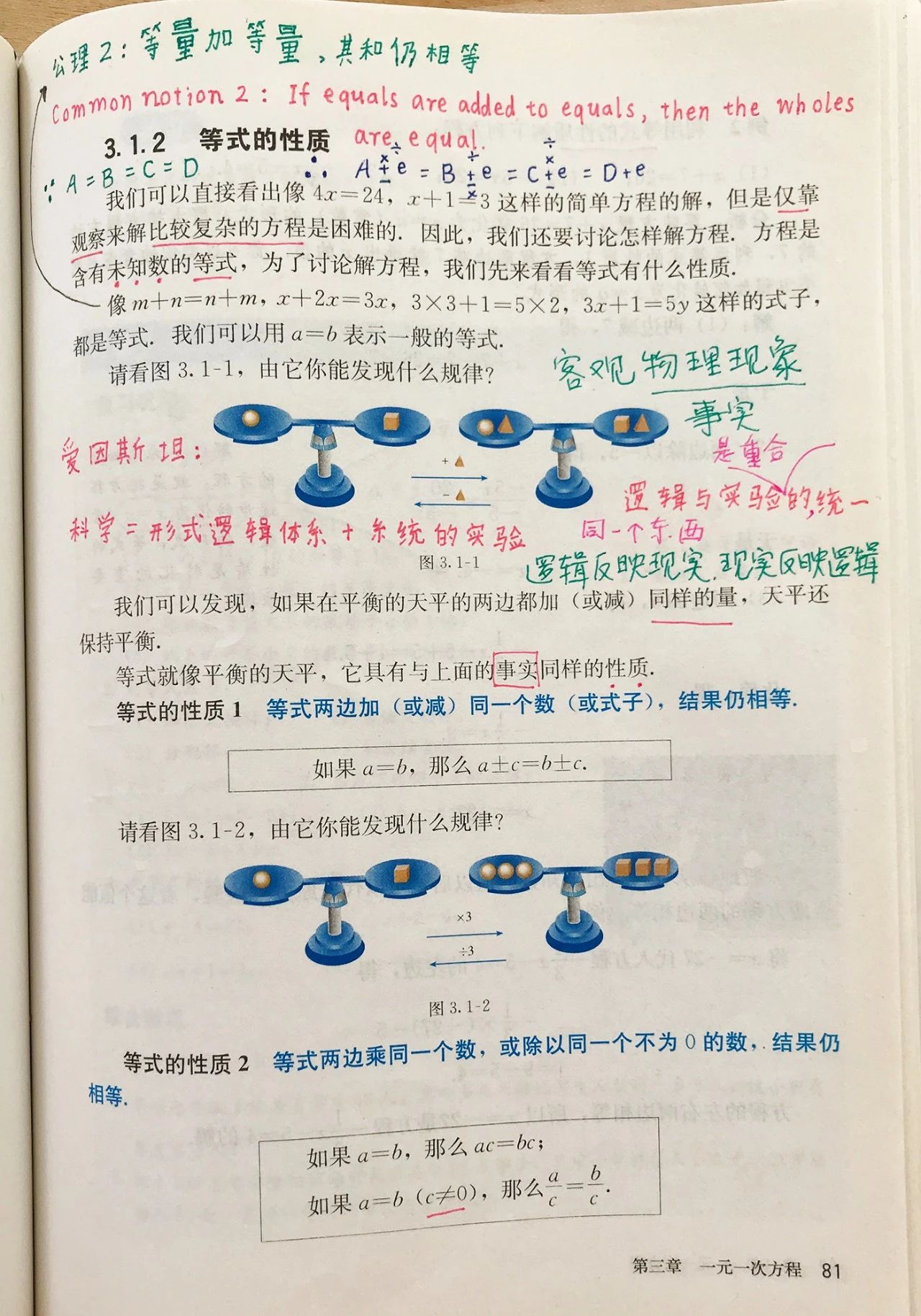
公理2：等量加等量，其和仍相等。

COMMON NOTIONS 2：If equals be added to equals, the wholes are equal.（The Thirteen Books of Euclid's Elements.by Euclid(Author), T.L.Heath(Translator)）

公理2：等量减等量，其差仍相等。

COMMON NOTIONS 3：If equals be subtracted from equals, the remainders are equal.（The Thirteen Books of Euclid's Elements.by Euclid(Author), T.L.Heath(Translator)）

《几何原本 》中的公理2和公理3将天平现象演绎得淋漓尽致，这是人类心灵对客观世界规律的归纳总结，然而课本还是只字未提“公理”二字，公理才是方程背后最为根本的数学原理。

爱因斯坦：西方科学的发展是以两个伟大的成就为基础的：希腊哲学家（在欧几里得几何学中）发明了形式逻辑体系，以及（在文艺复兴时期）发现通过系统的实验有可能找出因果关系。在我看来，人们不必对中国圣贤没能做出这些进步感到惊讶。这些发现竟然被做出来了才是令人惊讶的。（1953年爱因斯坦致斯威泽（J.E.Switzer）的信）

W·海森伯：对于原子物理学家，“物自体”最终是一 种数学结构，如果他一定要使用“物自作”这个概念的话；但是这种 数学结构——与康德相反——是间接地从经验推导出来的。（W·海森伯：《物理学和哲学》，范岱年 译）

“移项”这种解释本身就是错误的，用“相当于”解释“移项”这种现象也不太准确。

为了解题快，你把它当成公式或者规律背是可以的，但不能把它当成原理讲，当原理讲容易让人误解为是两边的量是真的被移动了。

头条百科的解释是“...像是移动了...”，比课本的解释要合理一些：

为什么船在顺流中行驶的速度会比船在逆流中行驶的速度快呢？

这种问题要用到力学上的知识才能够解释得清楚，建议课本在合适的地方加入相应的力学知识。连小学课本都加入了力学知识：《让 阿基米德&华罗庚&方舟子&老中医 教广大师生 学习方法&思想方式》。

陈省身：我觉得物理学里有很多重要的工作，是物理学家要证明说物理就是几何。比方说，你从牛顿的第二运动定律开始。牛顿的第二定律说，F=ma，F是力，m是质量，a是加速度，加速度我们现在叫曲率。所以右边这一项是几何量，而力当然是物理量。所以牛顿费了半天劲，他只是说物理就是几何。我觉得物理学里有很多重要的工作，是物理学家要证明说物理就是几何。比方说，你从牛顿的第二运动定律开始。牛顿的第二定律说，F=ma，F是力，m是质量，a是加速度，加速度我们现在叫曲率。所以右边这一项是几何量，而力当然是物理量。所以牛顿费了半天劲，他只是说物理就是几何。不但如此，爱因斯坦的广义相对论也是这样。爱因斯坦的广义相对论的方程说......你仔细想想，他的左边是几何量，是从黎曼度量得出来的一些曲率。所以爱因斯坦的重要方程式也就是说，几何量等于物理量。

Law 2 ：A change in motion is proportional to the motive force impressed and takes place along the straight line in which that force is impressed.【The Principia : Mathematical Principles of Natural Philosophy. by Isaac Newton (Author), I. Bernard Cohen (Translator), Anne Whitman (Translator),Julia Budenz (Translator)】

课本说：“当时的埃及人如果采用了这种形式，它一定是‘最早’的方程”

课本在这里是否出错了？与《数学辞海》不一致，首先等号的右边不是33，而是37，然后《数学辞海》说：“这是迄今发现的最早的方程”：

▲《数学辞海》（第一卷 Vol1）(全六卷) by 裘光明 等数学辞海总编辑委员会

上边这种情况，“遇到有分母的时先去掉分母”，可能很多人都觉得这是理所当然的。

当然，用最简易的推理就能推出我们必须要做去掉分母这个环节，因为不去分母的话，我们永远都解不开这种方程，我们永远都到达不了x = a 这种形式。但课本并没有从理论上阐释为什么要通过去掉分母这一程序才能够到达x = a 这种形式，没有解释先去分母为什么就是合理的。

数学思想是严谨的，课本有必要在此处或在其他相应的地方展开论证，或者是至少提醒一下，为什么一定要先去掉分母：

乐乐在用（3a+1）/ 2 - 2 =1/2 x （3a + 1）- 2 = 3ax1/2 + 1/2 -2说明了这种顺序，就是说就算我们把（3a+1）/ 2 拆分成了3ax1/2 + 1/2 -2，按照计算的顺序还是得先从3ax1/2 + 1/2算起，也就是说先算（3a+1）/ 2是计算法则导致的结果。

所以，算上边那种方程，程序是先去掉分母，因为有分母的算式其实是除法运算，除法算式又可被看成是一个数乘以另一个数的倒数，所以有分母的式子其实都是乘法算式，运算法则是先算乘法：

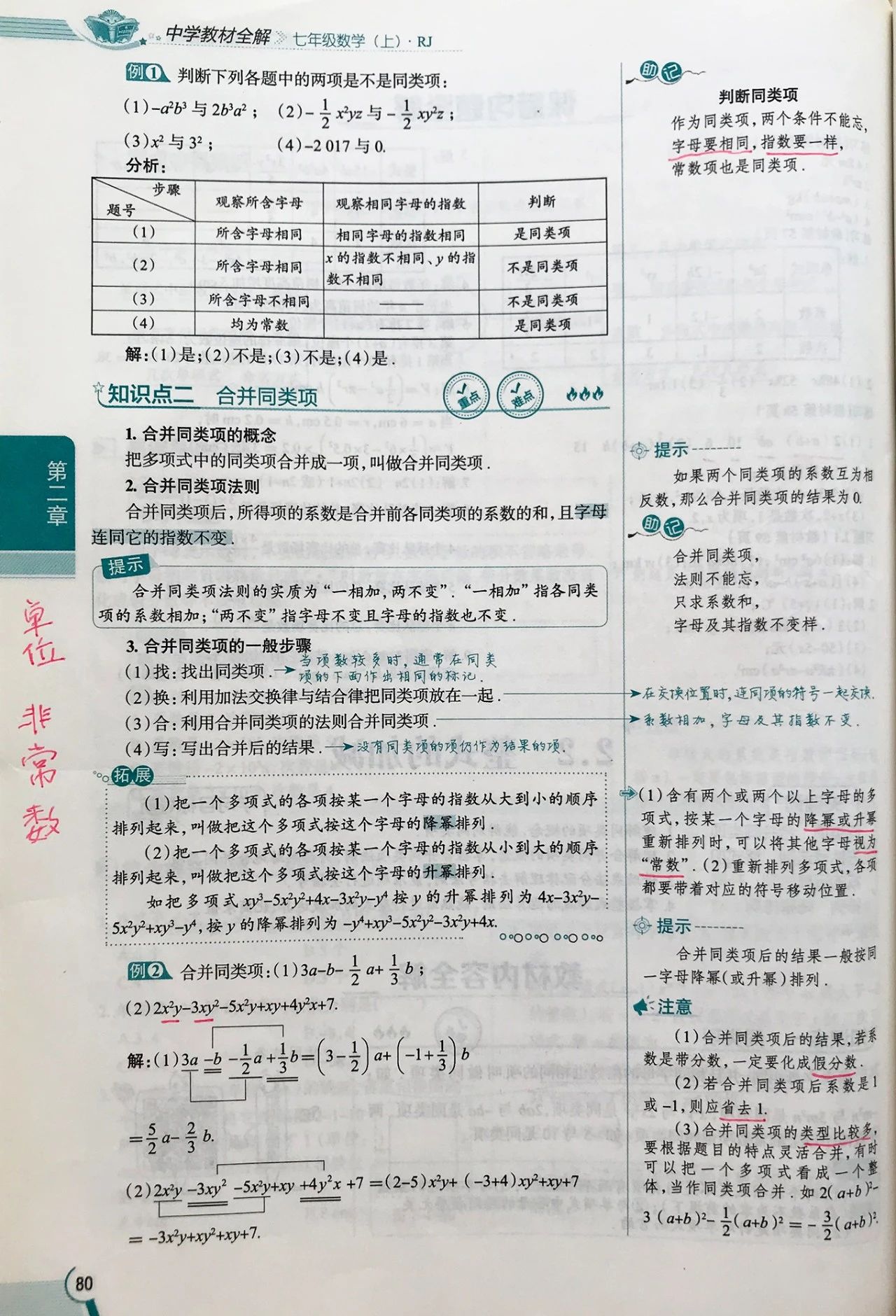
课本对这个“同类项”概念没有解释本质含义，这样很不好，这样很不严谨。

因此薛大侠主编的《全解》解释说：含有两个或两个以上字母的多项式，按某一个字母降幂或升幂重新排列时，可以将其他字母视为“常数”。

虽然“常数”打了引号，但也不能这样说，因为常数不是什么乱七八糟的数字：

其实问题的根源还在于如何认识单位这种在数学中最基础的东西，乐乐在课本页面的批注里已有所解释了：

其实从小学到中学，课本一直都没有将“单位”到底是个啥东西解释清楚，所以教材往后编写的过程中才会出现遇到单位就语义模糊、概念不清这种情况。还是《原本》对单位的定义和解释最为清晰：

▲The Thirteen Books of Euclid's Elements.by Euclid，兰纪正译

由于之前对单位概念的解释一直都不够清晰，课本在讲绝对值时，给出的解释就会不够透彻，其实绝对值的本质意义是度量单位（unit of measure）恒定：

Wikipedia：In 1806, Jean-Robert Argand introduced the term module, meaning unit of measure in French, specifically for the complex absolute value......

单位方面的问题，在自然创意设计的文章《关于网红李永乐老师对质数、合数概念之理解被程良伟老师批评指正》中有所涉及。

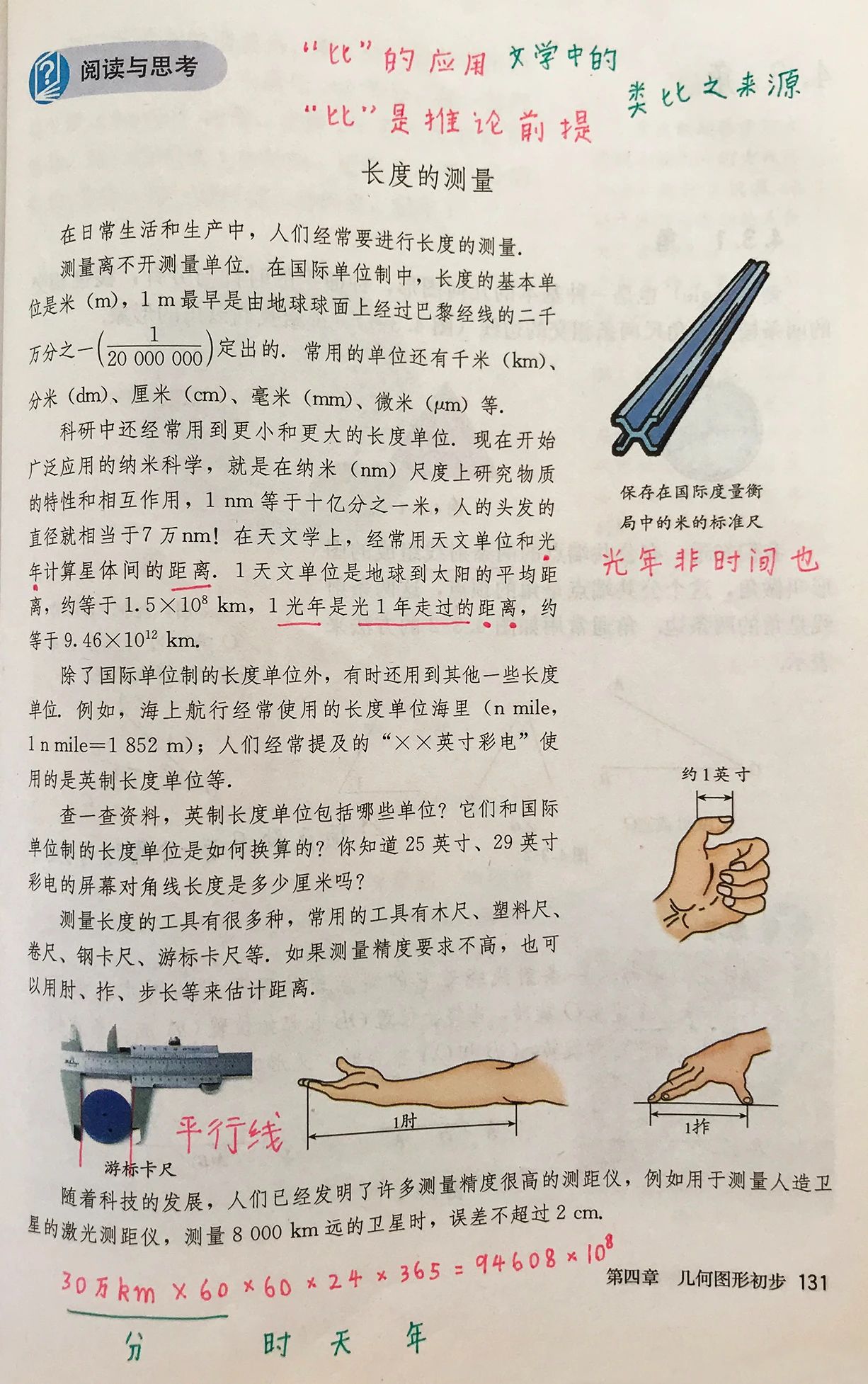
阿基米德是“科学计数法”的发明者，这么厉害的发明创造课本为什么不提？难道是编写教材的老师们不知道是谁发明了科学计数法吗？

▲The Works of Archimedes . by Archimedes (Author), T.L.Heath(Translator)

▲维基百科：菲尔兹奖正面刻有阿基米德的头像，拉丁文意为“超越他的心灵，掌握世界”

▲维基百科：菲尔兹奖背面的拉丁文意为“聚集自全球的数学家，为了杰出著作颁发（奖项）”

批评完了，说点表扬的

人教版《七年级数学上册》里边的课后习题还是很不错的，其中的每一道题目几乎都经过了精心的挑选，它们归纳和演绎了概念之间的各种关系各种情况，几乎没有重复的。虽然题都不是非常难，但大多数题目都是可以用不同的思路和方法去解的，它们会引导孩子们从不同的角度去探索和理解基础概念，通过反复思考和练习之后，定能使孩子们深入理解数学概念。

那些练习册和试卷里的习题基本都是你抄我，我抄你，与课本中的题型都是大同小异，大多数练习册都是编辑在短时间内东拼西凑搞出来的东西，课外的习题没有经历如课本习题所经受过的大浪淘沙般的层层筛选。如果能将课本中的经典题型消化吸收并融会贯通，应对外边的题目根本就不会有啥问题。如果一定要额外加做题目，筛选一些课本中没有的难题和怪题才合理，而不是本末倒置刷大量重复性的题目，企图把啥都当成套路折腾是耗费精力浪费时间。

所以一定要狠狠地批判家委会和学校的老师

估计网上很多人都没有仔细研究过课本里的题目，他们根本就不了解实际情况，就瞎胡说瞎起哄，说什么数学课本里的题都太简单了，只做课本里的题会打不开思路，过不了考试关。估计大多数学校的老师，以及大多数家长也都是以此谬论为依据，才采取了错误的教学方式：他们给学生购买各种大堆的练习册和试卷，使学生陷入题海。

丘成桐：......开始时有些紧张，因为学生比以前上课时更加投入。我没有打算说很多话，但其他同学则踊跃发言，似乎头头是道。几个星期后，我把课本（就是斯帕尼尔本人编写的）看了一大半，发觉大部分同学都是在吹牛瞎说。（丘成桐：《我的几何人生》）

乐乐在过去的六年小学期间，据说老师给语数英都只各买了一本练习册，但家委会又让老师们给这三门功课各增加了一本练习册，这种“策略”让作业量陡然倍增，加之三门功课每个月的月考要重复考试两次以上（曾见识过他们一门功课的月考重复4次之多），大量的试卷堆砌起来可算作另一本练习册，算下来实际上每门功课都做了三大本练习册，加之还要做课本中的练习题，每门功课就做了4本练习册，每学期总计要做：3门功课 x 4本练习册 =12本习题集。6年合计：6年 x 2学期 x 3门功课 x 4本练习册 = 144 本习题集，减掉一、二年级没有英语作业，144本习题集 - 2年 x 2学期 x 4本练习册 =128 本习题集，但是还得加上6次寒假和5次暑假的作业...

研究课本和课后习题的时间被挤压没了，这哪里是什么“策略”，这简直就是舍本逐末，找虐找罪受。最佳的学习策略应该是让孩子们把闲余的时间用来给课本“找错误”

亚里士多德：吾爱吾师柏拉图，胜于余物，然吾爱真理，胜于吾师。

学习语数英，6年做了一百几十本练习册，浪费了太多的时间和精力，如果规划利用好这些时间的话，可以学成很多有意思的专业和技能。

如果按每个学期浪费掉了两个月计算的话，这6年的12个学期一共浪费了24个月，24 ÷ 4（一学期按4个月计算）= 6（个学期），这6个学期不就是读3年初中的时间嘛，浪费掉的时间和精力可以读完初中了

袁岚峰：我们现在一个非常大的弊端，就是小学、中学人为地压低了学习的速度，让许多人以为只能按照这种蜗牛一般的速度来学习。我的感觉是，并不需要特别出类拔萃的智力，只需要正常的智力，一路学到初中的数学并不需要太长的时间，大多数孩子应该都能学会。这其实是最节约时间、最适合培养人才的做法。但很可惜的是，我们的教育部门并没有这么做，反而宁可用低水平的重复刷题占满学生的时间，浪费他们好奇心和记忆力最强、最适合学习的年华。这实在是我不能理解的。

苏步青：我青年时代学数学，就养成多解题的习惯。我首先把教科书上的规定的习题，通过自己独立思考把它解出来，从中领会其所依据的是什么基本概念，什么定理，然后思考是否还能用别的方法解题，把这道习题真正搞懂。有一次，我曾用大同小异的二十种方法解一道习题，互相比较，从中找出最简便的一种方法。由于基本功扎实了，后来我在演算其它题目时，就感到运用自如。

但是，目前有人对解题的意义认识有偏差，以为题目做得越多，考试命中率就越高。于是家长、老师忙于收集各类习题，历届高考试题，竞赛题，外国中学生试题等，统统要求学生做出来，幻想从中碰上升学的试题。这种“题海战术”式的训练，对提高学习成绩收效甚微。其实，每年高考，数学试题的类型就那么一些，但题目却变化万千。你做这题，他出那题，完全相同的题几乎没有。如果定理不熟，不会应用，有时看上去像是“对上号”，结果还是要解错的。所以，“题海战术”只能加重学生的负担，不利于学生的健康成长，不可能真正提高教学质量。前几年，我收到一位外省青年学生寄来十公斤重的笔记本，打开一看，全是数学习题解答，起码有七八千道。他附言说，自己解了这么多习题，数学高考还是考不好，身体也搞坏了，这件事足以发人深省。（苏步青：《谈谈数学打基础问题》）

陈钱林把博客关闭之前，我看过他记录的他儿子陈杳的备考策略：要以课本和《全解》（读全解是为了深入理解知识点）为主，而不是以刷海量习题为主导。

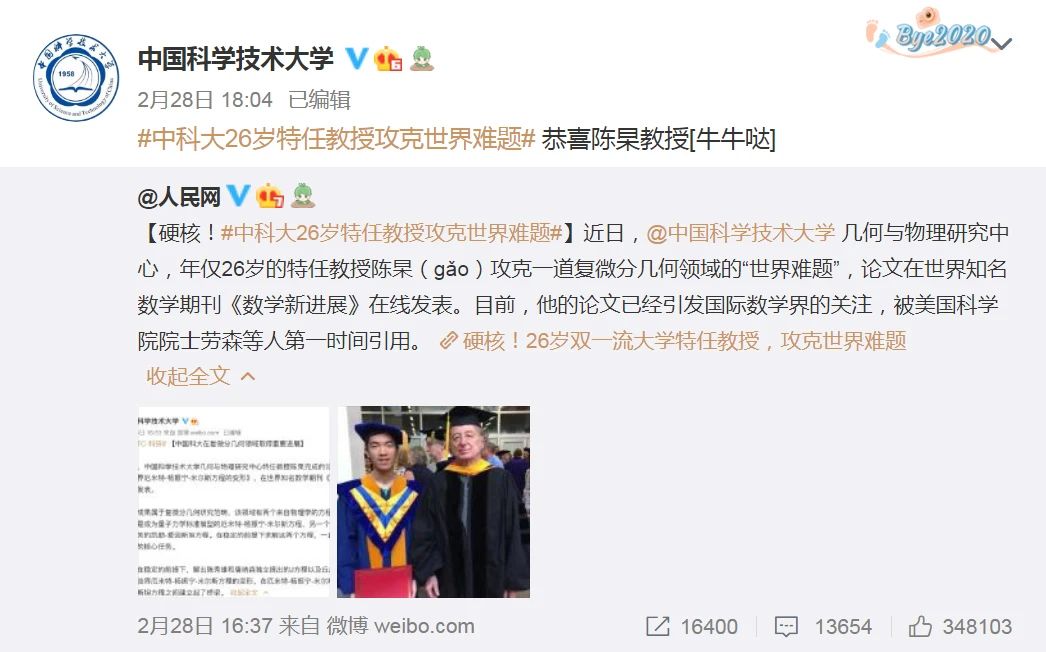
▲中国科学技术大学，年仅26岁的特任教授陈杲（gǎo）攻克一道复微分几何领域的“世界难题”

如果想知道更多陈杳的学习方法，可点击阅读自然创意设计的文章《如果让陈杲和陈杳 多做作业 少自学，他们还会很厉害很成功吗？》。

▲“双减”意见

中国学生的兴趣没有外国学生大。外国学生有想法、有创意......我觉得是老师没教好。比如学奥数，最好是因为有兴趣而学，而不要把全部时间都放在考试上......老师填鸭式的教育，让学生变成了一个考试机器。不停教你解题方法，让你一碰到题就自动反应，基本不用想。所以学生就没有思考能力了，而思考能力对我们来讲是最重要的。（提问丘成桐：疫情来了，还要去留学吗？）

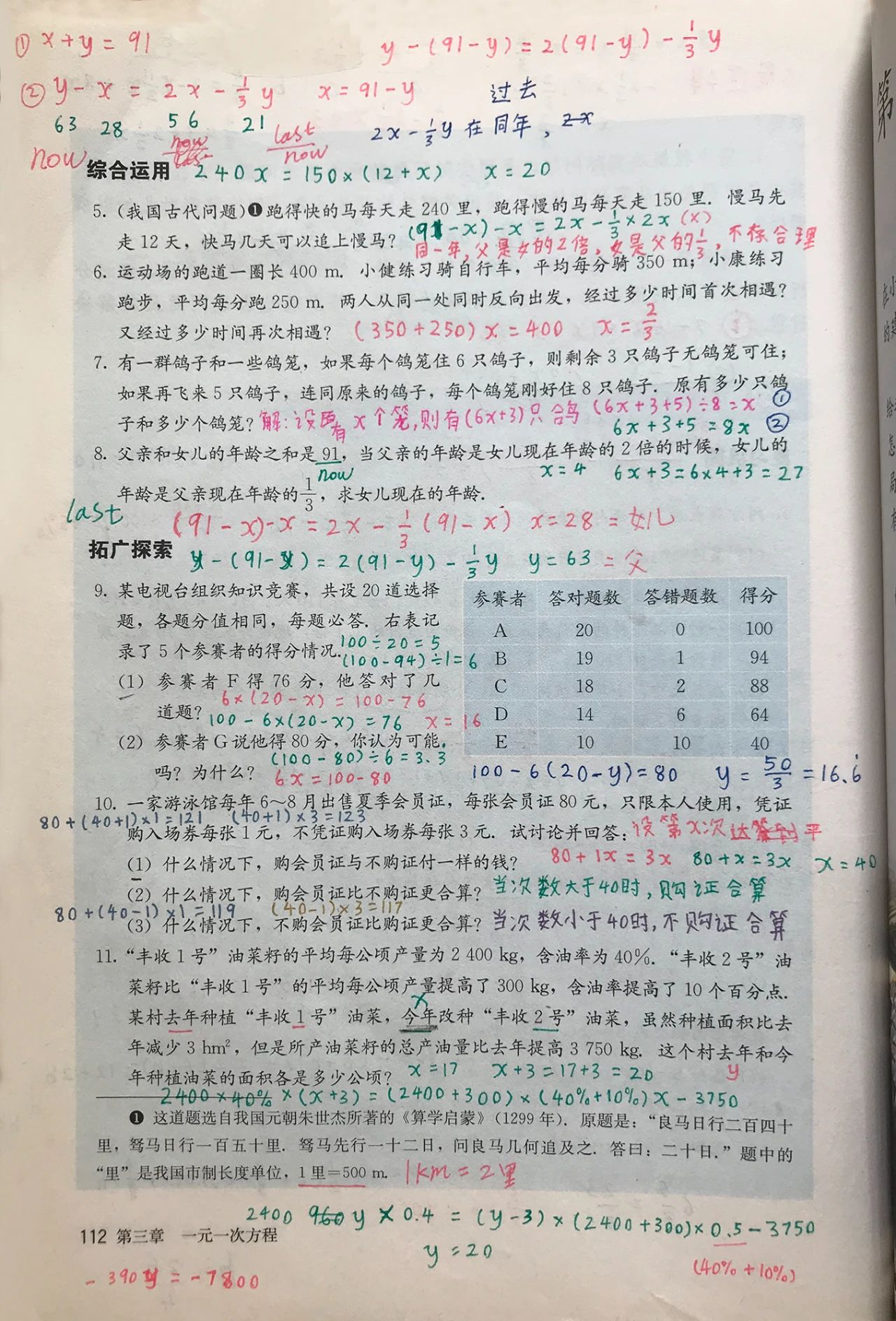
下边是一些被乐乐解开了的习题，它们只是整体课本习题中的一小丁点：

华罗庚：应该怎样学会读书呢？我觉得，在学习书本上的每一个问题，每一章节的时候，首先应该不只看到书面上，而且还要看到书背后的东西.这就是说，对书本的某些原理、定律、公式，我们在学习的时候，不仅应该记住它的结论，懂得它的道理，而且还应该设想一下人家是怎样想出来的，经过多少曲折，攻破多少关键，才得出这个结论的.而且还不妨进一步设想一下，如果书本上还没有作出结论，我自己设身处地，应该怎样去得出这个结论？

我们只有了解结论是怎样得来的，才能真正懂得结论.只有不仅知其然，而且还知其所以然，才能够对问题有透彻的了解.而要做到这点，就要求我们对书本中的每一个问题，一天没有学懂，就要再研习一天，一章没懂，就不要轻易去学第二章.这样学虽然慢些，但却能收到实效.我在年青时，看书就犯过急躁的毛病，手拿一本书几下就看完了.最初看来似乎有成绩，而一旦应用时，却是一锅夹生饭，不能运用自如了.好在我当时仅有很少的几本书，我接受了教训，又将原书不断深入地学习(注意，并不是“简单地重复”)，才真正有所进益。

（华罗庚：《聪明在于勤奋 天才在于积累—— 数学大师华罗庚谈怎样学好数学》）

最后说明一下，文章里的习题都是乐乐做的，页面上的批注和阐释也都是他写的，其中的推理少不了他的贡献，所以他也是文章的作者。