【数据分析岗】机器学习(二)
发布于 2021-09-07 11:21 ,所属分类:2021面试经验技巧分享
 【数据分析岗】机器学习(一)
【数据分析岗】机器学习(一) 先上框架性原理,再结合真题操练。
先上框架性原理,再结合真题操练。本篇先详细讲解主流降维算法的原理,
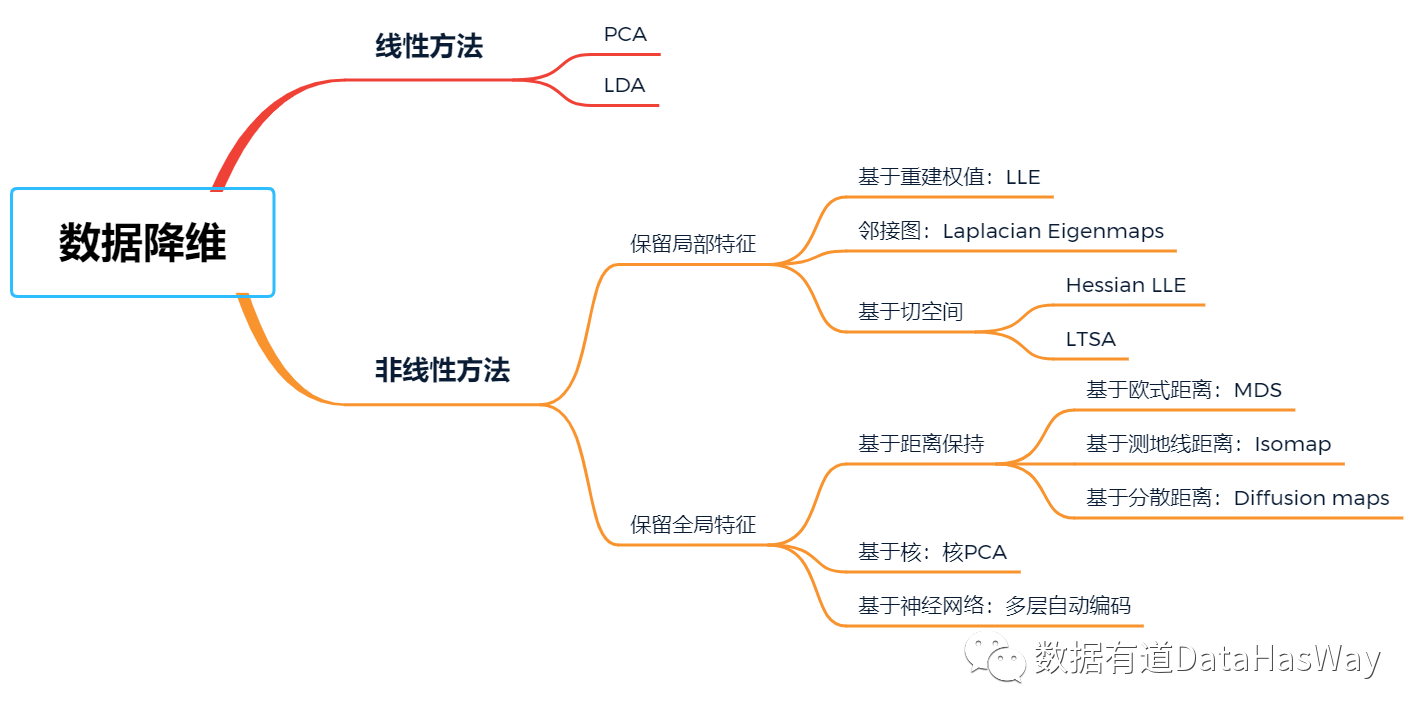
一、
常见降维算法
01
主成分分析
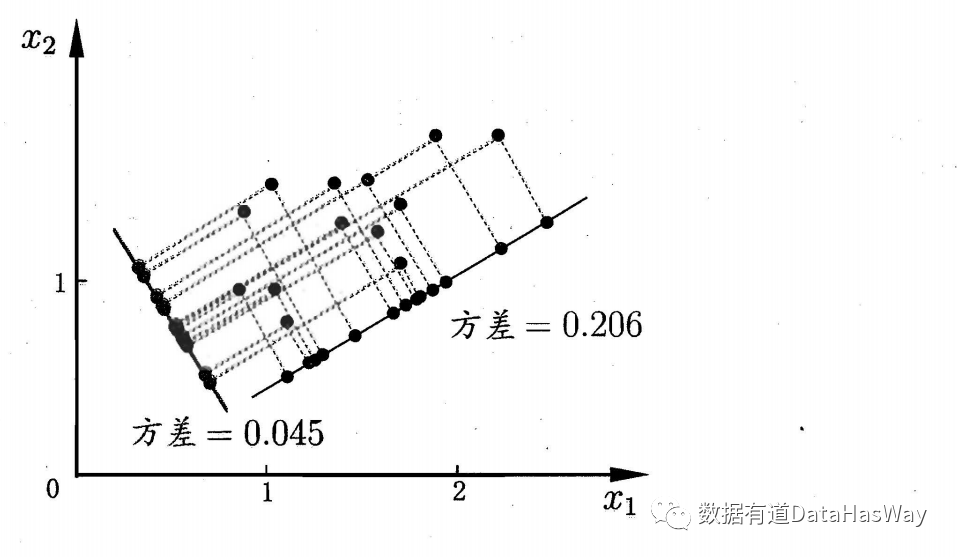
最近重构性:样本点到这个超平面的距离都足够近
最大可分性:样本点在这个超平面的投影能尽可能分开
基于最近重构性和最大可分性,能分别得到主成分分析的两种等价推导。
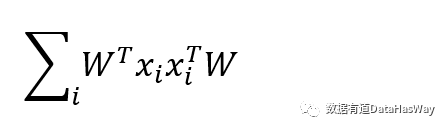
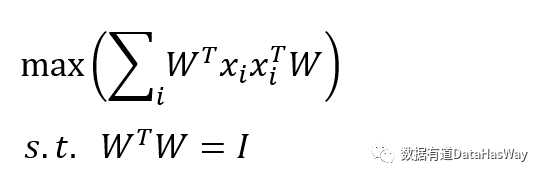
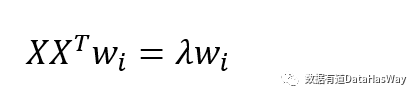
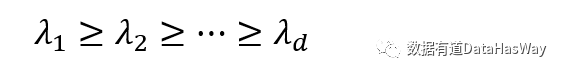
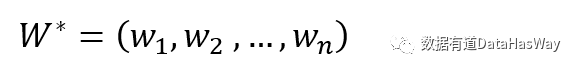
02
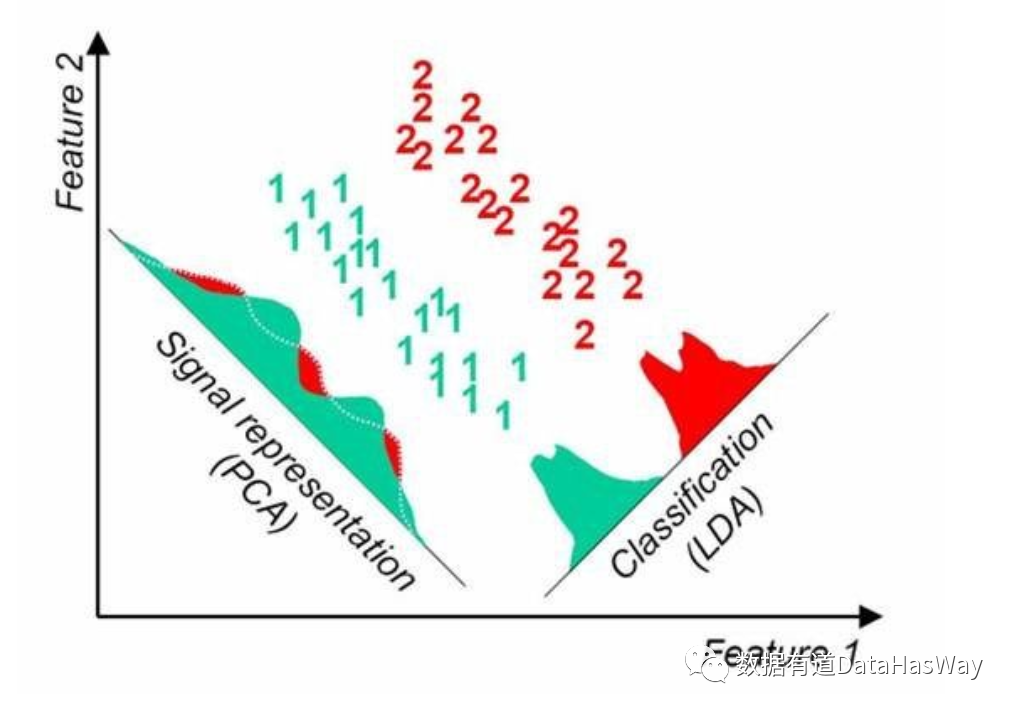
LDA降维方法
LDA是一种监督学习的降维技术,即,它的数据集的每个样本是有类别输出的。
03
局部线性嵌入(LLE)
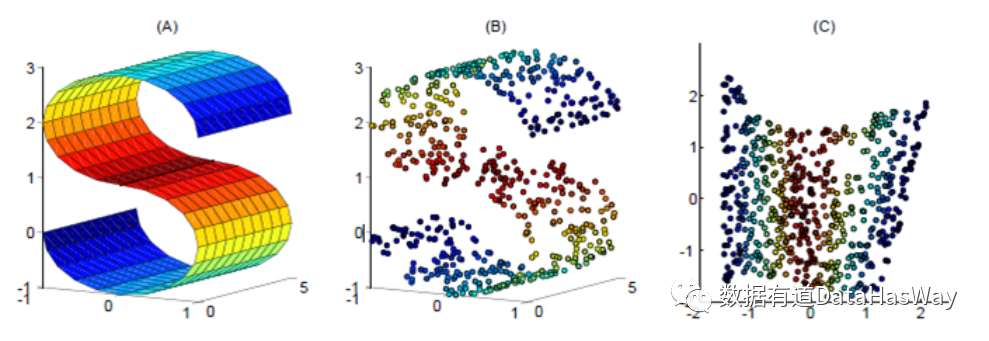
LLE算法认为每一个数据点都可以由其近邻点的线性加权组合构造得到。
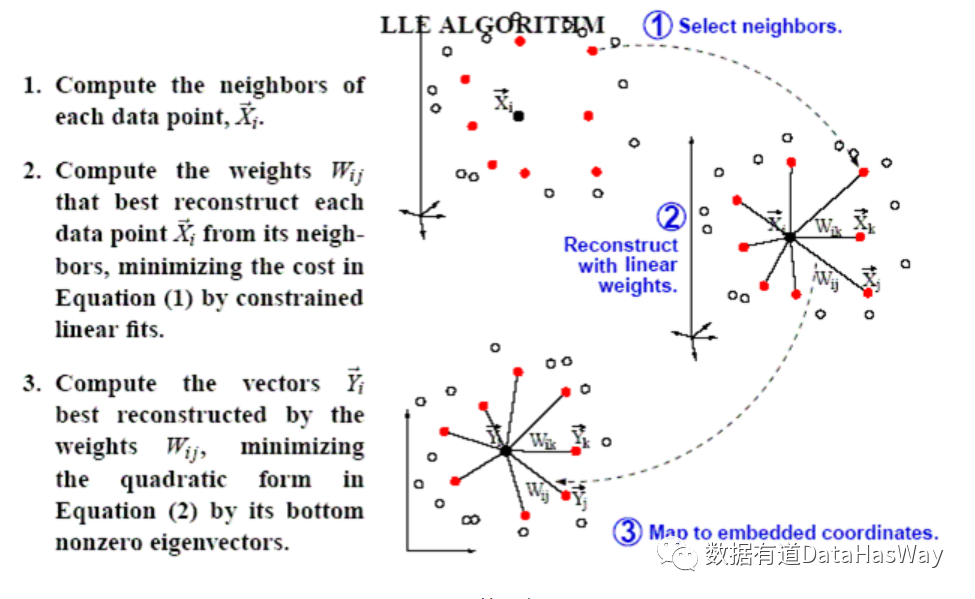
04
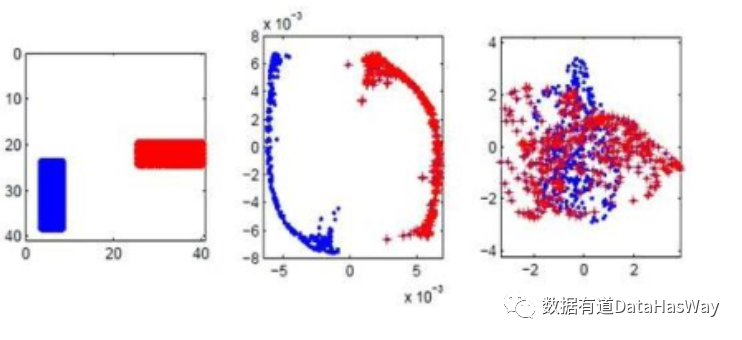
LaplacianEigenmaps
二、
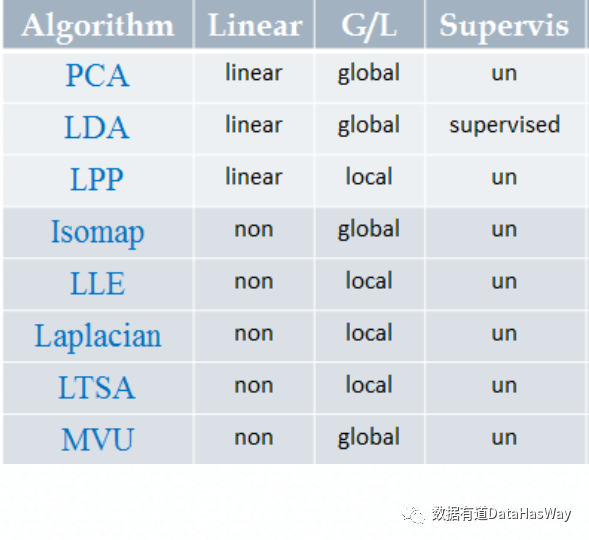
降维算法比较
三、
经典笔面试题
使得数据更容易使用 减少输入的变量个数量,降低算法的计算开销 去除噪声 使得结果容易理解
新组成的数据不具有可解释性;
降维的维数需要事先指定。
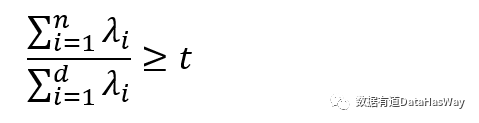
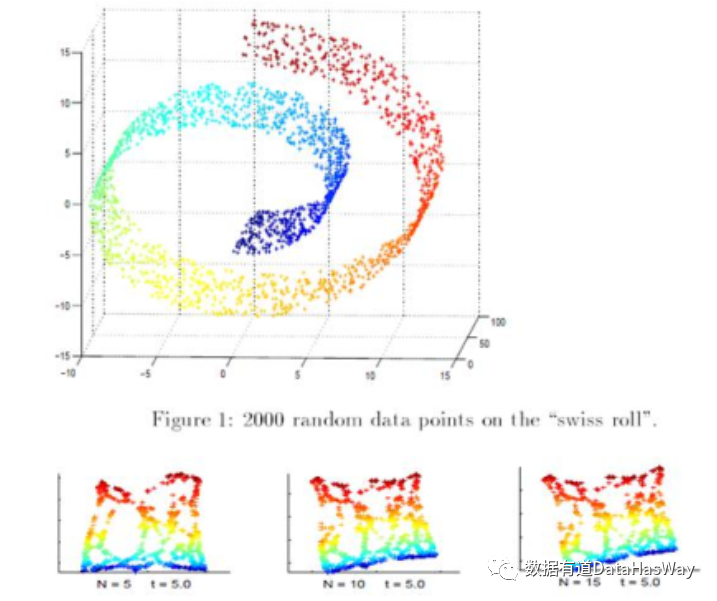
非线性的降维方法
降维的同时保留了局部近邻节点的信息 属于流形学习
LE算法的局部特征保留特性使得它对孤立点和噪音不会那么敏感;
算法基于流形的内在几何结构,因此它展示出嵌入的稳定性,只要嵌入是等度量的(Isometric),这个表示就是不变的。



 欢迎
欢迎





![[Python] 超强大的Python数据分析课程-偏机器学习方向 Python数据分析经典案例课](https://static.kouhao8.com/sucaidashi/xkbb/c5d2bb19e1f9dd55f599179051f766e3.jpg?x-oss-process=image/format,webp/resize,w_88/crop,w_88,h_88,g_nw)
![[数据分析] 2017最新唐宇迪 Python数据分析与机器学习实战视频教程](https://static.kouhao8.com/sucaidashi/xkbb/f4240cce2576c29c67fa506be08f5a39.jpg?x-oss-process=image/format,webp/resize,w_88/crop,w_88,h_88,g_nw)



![[Python] 超强大的Python数据分析课程-偏机器学习方向 Python数据分析经典案例课程](https://static.kouhao8.com/sucaidashi/xkbb/5a99c55b14486fd1d6a7788be5b4a940.jpg?x-oss-process=image/format,webp/resize,w_88/crop,w_88,h_88,g_nw)
![[Python] 超强大的Python数据分析课程-偏机器学习方向 Python数据分析经典案例课程](https://static.kouhao8.com/sucaidashi/xkbb/eba0756ede2ec568a9d48a79842c9979.jpg?x-oss-process=image/format,webp/resize,w_88/crop,w_88,h_88,g_nw)

![[机器学习/深度学习] 人工智能全新实战特训营-机器学习+人工智能+数据分析理论与实战教程 机器学习视频](https://static.kouhao8.com/sucaidashi/xkbb/9caec0936de2bd257a4f7b87f0dc83c3.jpg?x-oss-process=image/format,webp/resize,w_88/crop,w_88,h_88,g_nw)


![[Python] 高端实战 Python数据分析与机器学习实战 Numpy/Pandas/Matplotlib等常用库精讲](https://static.kouhao8.com/sucaidashi/xkbb/70d4b9f114bd46480d5aa16747689329.png?x-oss-process=image/format,webp/resize,w_88/crop,w_88,h_88,g_nw)
![[数据分析] 地产数据分析师课程全](https://static.kouhao8.com/sucaidashi/xkbb/c4da1071add9442d6ce8325ec6fc4221.jpg?x-oss-process=image/format,webp/resize,w_88/crop,w_88,h_88,g_nw)
![[大数据] 小象《金融数据分析》第二期](https://static.kouhao8.com/sucaidashi/xkbb/f82a7c9cc0e016a9b9ffb15690034b11.png?x-oss-process=image/format,webp/resize,w_88/crop,w_88,h_88,g_nw)


相关资源