听说新初一的数学联考哀嚎一片,咱来分析分析卷子
发布于 2021-11-14 17:46 ,所属分类:数学资料学习库

Rene Magritte
刚过去的新初一期中测试,有俩版本,S字头领衔的那波学校,测试难度上确实比另一波大一点,听说考的学生哀嚎一片,叫苦连天。
甚至传言内含不少超纲、甚至奥赛级别的题目!
为了验证这个说法真假,下午我找了一份做了做,从5点13到5点59,用时46分钟,错了三处:
一个没把人家原数字里的+号填上,数轴的箭头也没画,按3分扣;一个写了三分之三,没化简成1,1分;还有一个是真没想到,找个差不多的就填了,实实在在地错了,1分。
大概能考135。

这套卷子,要说真有啥难题,第8题、第16题、第23题第4小题、第24题的第2、3小题,这些题目加起来的分值大概有21分,其他的题目,真的是基础题,常规练习铁定能见到。
包括第22题,看起来完全平方公式的几何证法没学过,是初二内容,好像超纲了,但题目给出的条件都已经细致成那样了,问题也简单的不能再简单,明显是想考察现学现卖的自学能力。
如果一点都看不懂,那不该归罪于题目超纲,只能说自学能力实在是弱。
至于上面那几个看起来稍微难点的题目,咱一个个看,看看解决他们的思路是不是特别难?是不是上升到奥赛的层面了!
先看第8题,选择题最后一题:
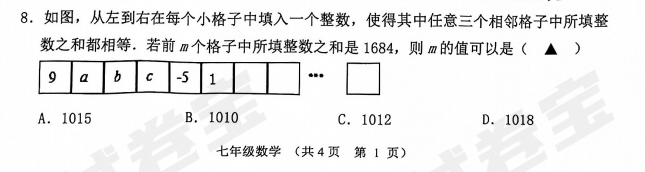
这道题,小学就做过,我随便出个题大家看下:
1、小明妈妈的笔记本电脑开机密码是六位数,只知道这个密码开头和结尾的数字分为是6和7,并且知道六位密码每相邻的三个数字和是16,你能破译这个密码么?(三年级的数字推理题)
再看第8题,知道9、-5、1以及相邻三个格子之和相等,求abc,跟上面这道题没区别吧?
好,求出abc分别是-5、1、9,之后,这道题就变成给了一组数字9、-5、1、9、-5、1......然后求前m个格子之和是1684时,m是几的问题?
这不就是周期问题么?还是三年级学的东西!
当然了,从题目形式上肯定比三年级的题目看起来复杂点,但好歹也是初一的孩子了,总不能连题型都出的跟三年级一个样儿吧。
再看第16题,填空题最后一题:

这种题,非要说是新思维里的,常规课内见不到,也不是不行。毕竟按照过往中考的调性,涉及到绝对值的题目,多半都是选择题里来个特别特别基础,计算题中再插一个一眼就可以看出答案的。
但这种题,放在一般考试的填空压轴题,真不算太过分。
这类题要是一点点去推,讨论abc的符号关系,再完全借着字母去推演,确实比较棘手、有点复杂,但作为填空题或者选择题,还有一种相当实用的分析方式——试数。
a+b+c=0,且abc>0,那么a=3,b=-2,c=-1行不行?完全满足条件!
于是,x=1-1-1=-1,y=3-3-3=-3,所以x²-y³=(-1)²-(-27)=28。
这么做,难么?不是很简单么,就是最基础的,将符合条件的、简单的数字带入某个代数式中运算而已,这种算超纲呢,还是奥赛呢?真的算不上!
聊完选择和填空的两个压轴小题,我们再看后面的大题:
第23题,倒数第二题第4小问:

这类型的题目,从小学三年级一直到高中都有,小学题长这样:
铁岭市出租车的起步价是7元(路程在3千米以内),超过3千米的路程,每千米2元(不足1千米的按1千米计算),张宇从家到学校大约6千米,坐出租车应该付多少钱?
至于高中就是列出分段函数、画出相应的函数图像了!
这一题之所以难,难在甲用户水费不足24元(即用水量不足12m³)时,情况比较复杂。
根据甲乙共用水30m³,如果甲用水不到10m³,那么,乙就会超过20m³,会涉及三种单价收费;如果甲用水在10-12之间,乙就不会超过20,只涉及两种单价收费。
所以,这题难在分类讨论上,难在能不能在一堆眼花缭乱的字母中间,梳理清楚分段关系上。
这一点,对于绝大多数孩子来说,都不容易,那怎么办?四年级上册教过——列表法!
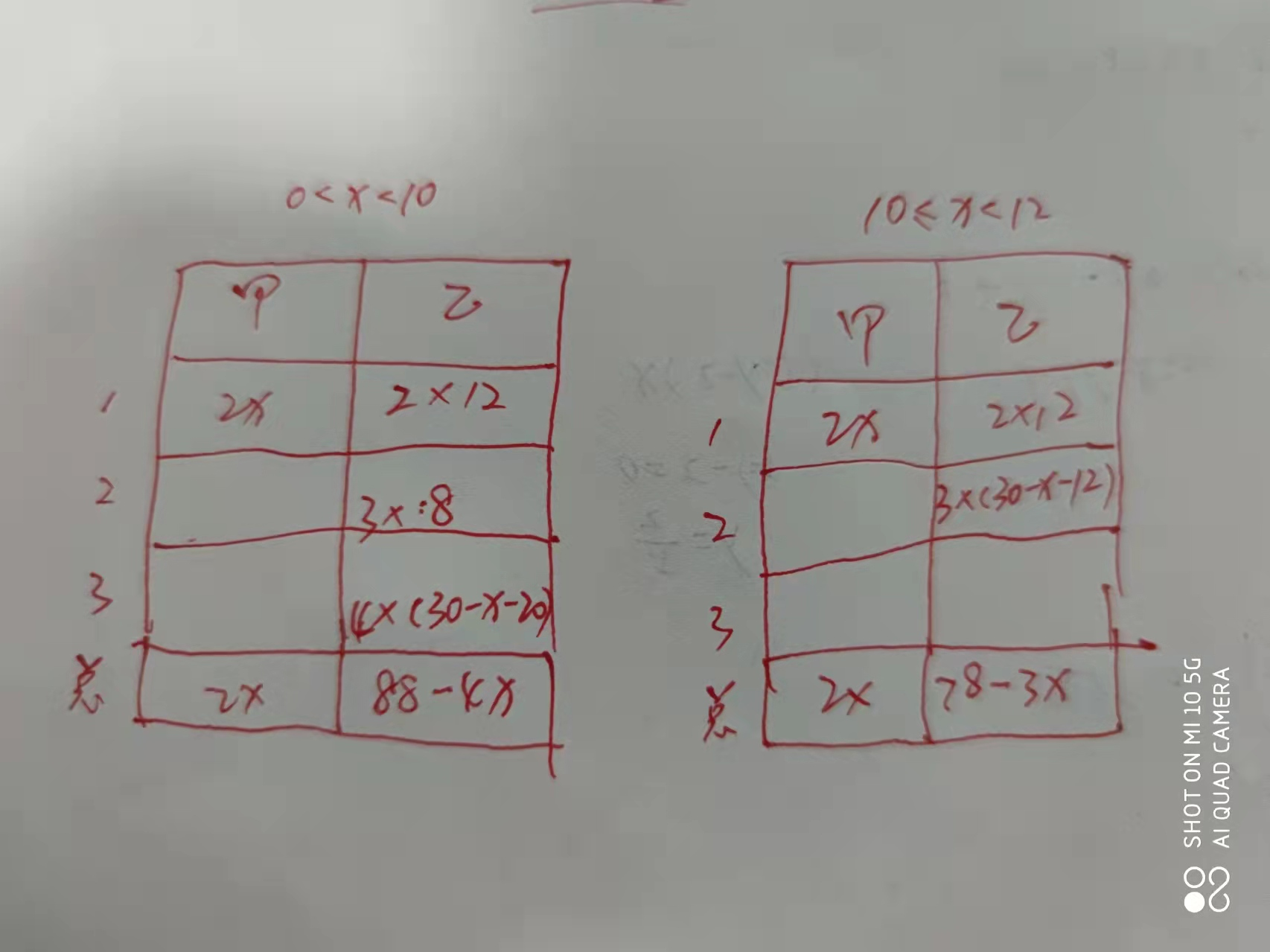
面对这么乱的关系,我如果只靠脑子想,也多半理不清楚,但只要动手列个表,把各种情况和数值挨个填入表格,汇总起来不是很清晰么?
可是,有几个孩子做这题的时候能想起来列表呢?估计寥寥无几!
这可是四年级上册数学教材中《解决问题策略》这一单元教的内容,是课内基础内容,到了初中,估计没几个还记得有这玩意的存在,为啥?
以我的实际教学体验看,从学生到家长大多没人在意这玩意,哪怕我苦口婆心的劝诫,务必要重视,甚至有些题还刻意要求列表,但对于已经习惯刷题,把记住解题过程当目标的孩子来说,列表多麻烦啊,一眼可以看出解题过程,列啥列。
最终导致,简单的不稀罕列,复杂的根本想不起来列!
所以,客观说这题难不难,难!我估计绝大部分学生都理不清楚,但问题在哪儿?如果从四年级甚至更早的时候,就有意识的、刻意练习,如果能够熟练应用表格去梳理条件,是不是容易很多,清晰很多?
这可是小学四年级课内的东西啊,哎,说多了都是泪!
试卷最后一题第24题:
很新颖,这种题,既不算奥数、也不是超纲,谁都没学过,就看有没有能力利用全新的知识点,独立解决问题,是现在中高考乃至小升初特别流行的一类题。跟22题一样,只不过比22题更难一些:
具体看题:

啥叫最佳分解?我之前也没听过,但看他找最佳分解的过程,不就是去找因数么,这玩意学过啊,小学的。
只要找到因数之差的绝对值最小的那一对就行了。看懂这个,第一问就不难了。再看第二问:巴拉巴拉说了一堆,估计大多学生题目都没读懂,就一脸懵逼的放弃了。
简单来说,t这个两位数ab,交换完就变成ba了,如果ba-ab=54,你觉得这样的两位数都有谁?
按照前面的题目的分析调调,我又该说,这个的确不简单,但它确实也在小学出现过,而且三年级就有。
咱先说初中代数式解法,无疑是b×10+a-(a×10+b)=54,求出b-a=6,从而得出b、a分别为9、3,8、2,7、1,根据题意,原来两位数就是39、28、17。
再说小学的,先看一道题:
一个两位数,加上它十位数和个位数顺序颠倒后的两位数,和是88,这样的两位数一共有多少对?(个位数和十位数数字不同)
根据题意,AB+BA=88,找出来A+B=8的,总共有8、0;7、1;6、2;5、3;4、4,从中不难看到8、0和4、4不符合题意,所以最后答案就很清晰了。
同理,ba-ab=54,不难先得出b-a=5,那么,ba就是94、83、72、61,可是不对啊,94-49不等于54,对此,我们观察数字做个微调,由于减法牵扯借位,所以数字a可以调小1。
于是ba就可能是93、82、71、60,60不符合原题意,排除。那ab就是17、28、39,完事儿!
各位朋友 ,这个分析过程真的是小学的题目啊,虽然在小学肯定是奥数级别的,但也是低年级的奥数,到了初中总不至于还能够的上奥赛级别吧?
至此,第二问就此搞定。
至于第三问,无非就是在一群因数中,凑出两个最为接近的乘数,第二个空我错了,考虑不周,所以这题也不说啥了。
至此,整张试卷最难的几道题分析完毕,我们做个汇总:
这几个题加起来超过20分,如果都搞不定,肯定考不到120分以上。这几题难么?客观上说,确实算难题,不少孩子看到得懵逼。
但是每一道题,要么能拆解成小学三、四年级的题型,要么可以用小学三四年级课内教的分析方法去梳理题目,从而把复杂的问题梳理清楚。
所以,作为初中的题目,也不算太过分!
不少家长看完这套卷子,惊慌失措,这么难的卷子,以后没有课外辅导班的帮助,可咋办啊?
说实话,初中的确不好办,每天焦头烂额的疲于应付那么多门学科,很多底层能力真的是想补都不知从何补起,只能寄希望于多刷题、多背题,考试时见个差不多的,填个七七八八算了。
稍微综合点、新颖点,只能趴窝。
但小学家长们还有机会和时间,不妨从这套卷子里深思一二,尤其是第22题和第24题这种题型。以我实际教学体验看,大多孩子以目前小学的学习状态,包括很多成绩看起来还不错的、很听话的,进了初中都得歇菜。
有时候也不是老师不想教,而是训练这类题所要求的底层能力,与小学阶段家长的认知冲突相当严重。哪怕老师想在小学阶段就开始训练孩子这方面的能力,家长能不能接受,都是一个很大的问题。
关于这点,有空单独写一篇文章说明吧。
对了,肯定有朋友想要看试卷和答案的,不用转发,直接后台回复“试卷”两个字就行了......是gongzhong号后台,不是本文留言,谢谢!
























相关资源