研究参阅|SPSS统计分析之Goodman Kruskal's Gamma检验分析实例
发布于 2021-04-26 02:46 ,所属分类:知识学习综合资讯
研究中两个变量均为有序变量且都基于配对相符或不相符时,可以使用Goodman & Kruskal’s Gamma检验分析。例如,王老师收集了全班24名学生的课前预习和课堂表现情况,试图解释课前预习好坏与课堂表现好坏之间的关系。
目的和要求
目的
检验两个有序变量是否存在显著的相关关系。
要求
有两个有序变量且都基于配对相符或不相符(例如课前预习好坏与课堂表现好坏)。

原假设和对立假设
原假设(H0)
学生课前预习情况的好坏与课堂表现的好坏不存在显著的相关关系。
对立假设(H1)
学生课前预习情况的好坏与课堂表现的好坏存在显著的相关关系。
假设评价
Goodman & Kruskal’s Gamma检验分析对学生课前预习情况的好坏与课堂表现的好坏不存在显著相关关系的原假设进行检验,如果检验产生的结果在原假设正确时的可能性小于0.05,拒绝原假设,否则接受原假设。

SPSS中输入数据及分析
定义变量
在变量视图中将课前预习情况定义为prepare,“1”、“2”、“3”分别代表“好”、“中”、“差”;课堂表现情况定义为performance,“1”、“2”、“3”分别代表“好”、“中”、“差”。


输入数据
在数据视图中输入24名学生的课前预习和课堂表现情况。
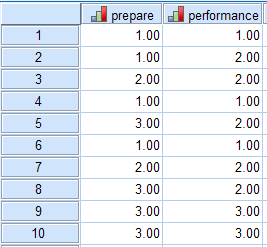
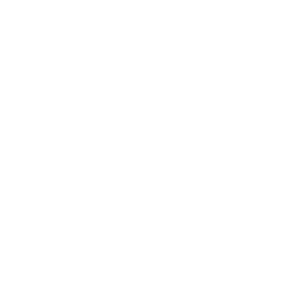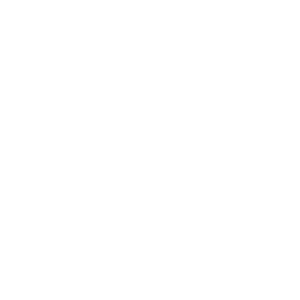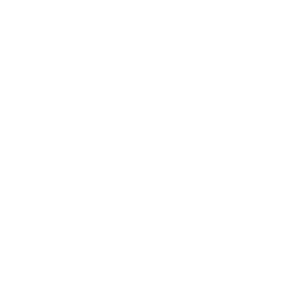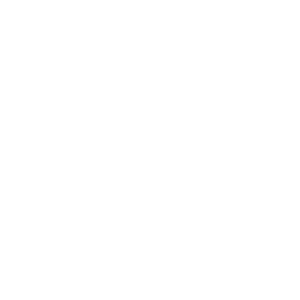
数据分析
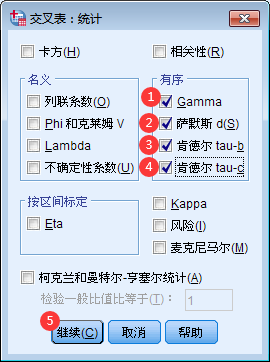
菜单栏中选择“分析>描述统计>交叉表…”,将课前预习情况选择到“行”框中、课堂表现情况选择到“列”框中;选择“统计”,选中“Gamma”、“萨摩斯(Somer’s d)”、“肯德尔 tau-b(Kendall’s tau-b)”、“肯德尔 tau-c(Kendall’s tau-c)”,点击“继续”;最后点击“确定”。
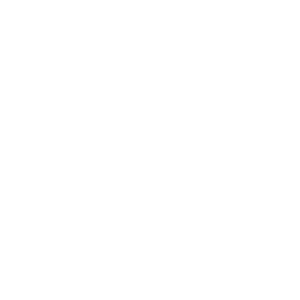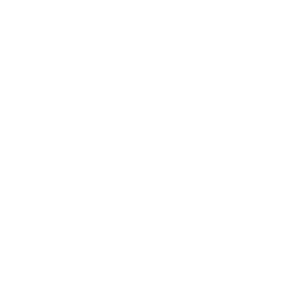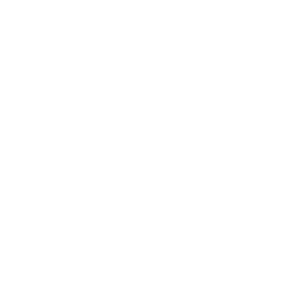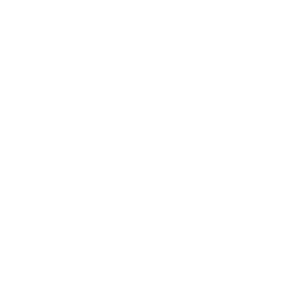

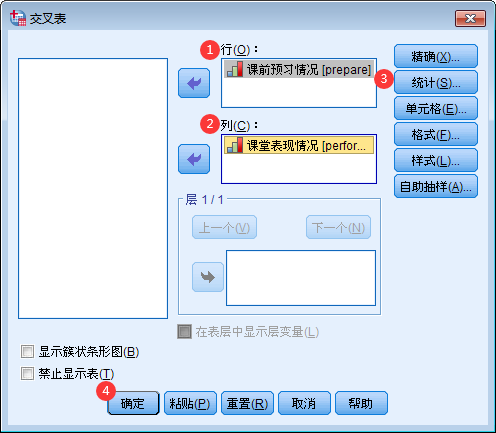

结果解读和效应量计算
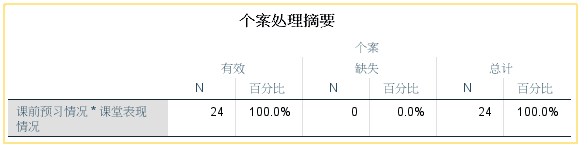
个案处理摘要表
显示了检验分析中数据处理的情况,可以看到有效个案数和缺失个案数。
交叉表
课前预习情况*课堂表现情况交叉表,以交叉表的形式显示了本研究的统计情况。
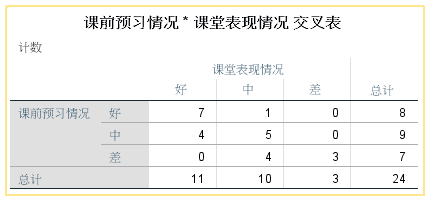
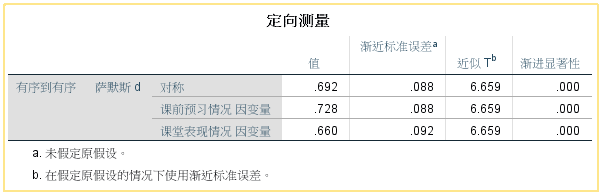
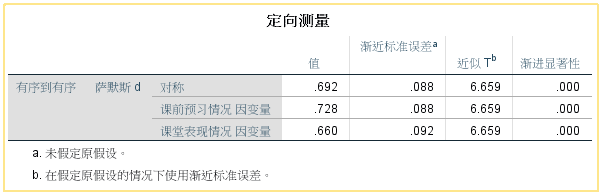
定向测量表
显示了有补偿配对的能力,用课前预习表现预测课堂表现时可减少66%的误差,用课堂表现预测课前表现预测是可减少72.8%的误差,并且显著性都小于0.05,表明两个变量都是很好的预测变量。
对称测量表
显示了研究的结果,显著性均小于0.05表明学生课前预习情况的好坏与课堂表现的好坏存在显著的相关关系;Goodman & Kruskal’s Gamma检验分析的结果Gamma(γ)为0.940表明显著的正相关,即课前预习情况越好课堂表现越好。
效应量计算
在Goodman & Kruskal’s Gamma检验分析中相关系数就是最常用的效应量,相关系数为±0.1、±0.3、±0.5,分别对应小、中和大的效应量。

问题和结果表述
研究问题
学生课前预习情况的好坏与课堂表现的好坏是否存在显著的相关关系?
结果表述
学生课前预习情况的好坏与课堂表现的好坏存在显著的正相关关系,课前预习情况越好课堂表现越好,γ(22)=0.940,p=0.000<0.05。







![[其他] R语言(统计分析、绘图)速成实战 快速学习 菜鸟速成 R速成实战(尹鸿)视频教程 x学堂](https://static.kouhao8.com/sucaidashi/xkbb/e6bbb88e61fa8e959d229a2bb8a86613.png?x-oss-process=image/format,webp/resize,w_88/crop,w_88,h_88,g_nw)
![[人工智能] 专业数据分析视频教程 SPSS视频教程(经典讲解+案例分析+数据处理+综合实例讲解](https://static.kouhao8.com/sucaidashi/xkbb/51ebc78bcfeae8be3fd9ae0d3aee4fa4.png?x-oss-process=image/format,webp/resize,w_88/crop,w_88,h_88,g_nw)





![[数据挖掘] 大数据分析师实战全集 数据挖掘与分析应用+电商数据化运营+轻松驾驭统计学+EXCEL](https://static.kouhao8.com/sucaidashi/xkbb/28d0d56e9273980c266a93f2a7ac17e0.png?x-oss-process=image/format,webp/resize,w_88/crop,w_88,h_88,g_nw)
![[教程] 量化投资之金融时间序列分析](https://static.kouhao8.com/sucaidashi/xkbb/d3f7ab080c69153bb5a5c56b25426148.jpg?x-oss-process=image/format,webp/resize,w_88/crop,w_88,h_88,g_nw)









![[数据分析] 地产数据分析师课程全](https://static.kouhao8.com/sucaidashi/xkbb/c4da1071add9442d6ce8325ec6fc4221.jpg?x-oss-process=image/format,webp/resize,w_88/crop,w_88,h_88,g_nw)


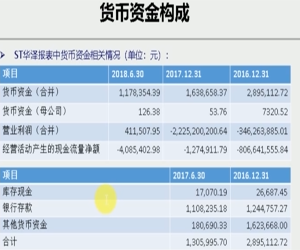

相关资源