【典型例题】等差数列求和

【典型例题】——等差数列求和

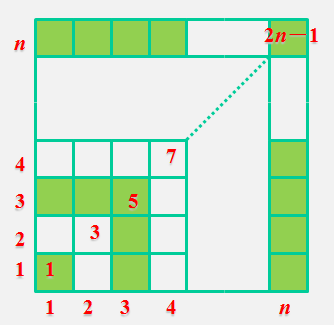
006．（13昭通）如图中每一个小方格的面积为1，则可根据面积计算得到如下算式：1＋3＋5＋7＋…＋（2n﹣1）＝ （用n表示，n是正整数）．

视频解析请点击：

【解析】

解：利用每个小方格的面积为1，可以得出：

1＋3＝4＝2²，1＋3＋5＝9＝3²，1＋3＋5＋7＝16＝4²，…，1＋3＋5＋7＋…＋（2n－1）＝n²．

故答案为：n²．

【总结】本题利用正方形的面积来求等差数列的前n项和，通过观察易发现每个数字周围的正方形数目都会等于这个数字，直接求出所有正方形的个数，即可求出面积，也可以利用高中等差数列前n项和的公式为S_n＝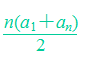
，代入公式得出结论．

【举一反三】

006．（13黔东南）观察规律：1＝1²；1＋3＝2²；1＋3＋5＝3²；1＋3＋5＋7＝4²；…，则1＋3＋5＋…＋2013的值是 ．

上一期【举一反三】解析：

005【解析】

解：第1个化合物的分子式CH₄，第2个化合物的分子式C₂H₆，第3个化合物的分子式C₃H₈，…，

增加一个C，就多两个H，第n个化合物有n个化合物的分子式为C_nH_2n＋2．

当n＝2013时，该化合物的分子式为：C₂₀₁₃H₄₀₂₈，

故答案为：C₂₀₁₃H₄₀₂₈．

【总结】本题利用了化学中烷烃这种化合物的分子式变化规律（其中CH₄是甲烷，C₂H₆是乙烷，C₃H₈是丙烷），可以发现这也是一个等差数列的规律．