函数的单调性

先回顾一下区间这个概念（毕竟课本表述得比我专业）

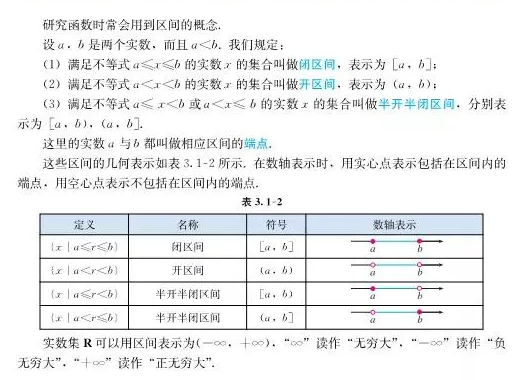
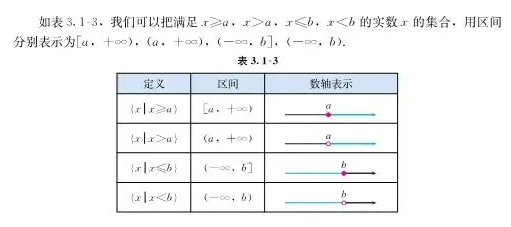
然后介绍今天的内容

一.函数的单调性

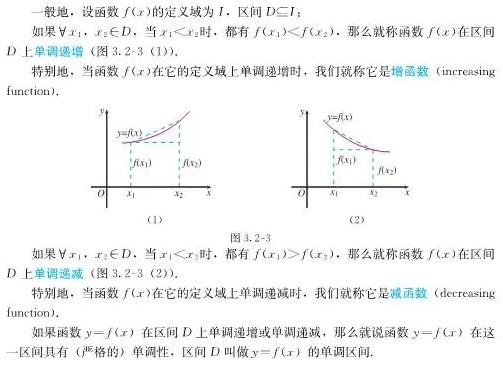
在我们学习导数之前，我们只能用定义法证明函数的单调性

方法如下（超麻烦，不过高一月考是肯定要考这个的）

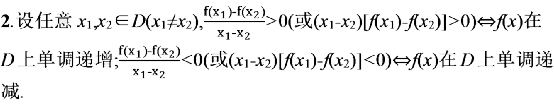
（1）讨论函数的单调性

判断函数单调性的四种方法:

(1)定义法;(2)图象法;(3)利用已知函数的单调性;(4)导数法.

2.证明函数在某区间上的单调性有两种方法:

(1)定义法:基本步骤为 取值 、 作差或作商 、 变形 、 判断.（重点介绍）

(2)可导函数可以利用导数证明.（求导暂不介绍）

3.复合函数单调性的判断方法:

复合函数y=f (g(x) )的单调性,应根据外层函数y=f (t )和内层函数t=g(x)的单调性判断,遵循“同增异减”的原则.

（2）求函数的单调区间

例题：函数f(x)=|x²-3x+2|的单调递增区间是(　　)

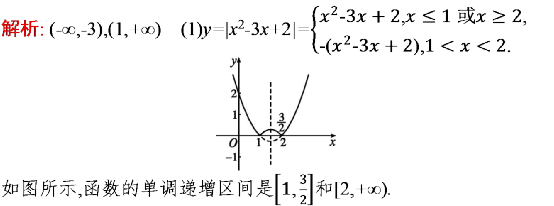
数形结合，把图像画出来，深刻理解绝对值的含义，把x轴下面的部分翻上来即可得出答案。

求函数的单调区间与确定函数单调性的方法一致,常用以下方法:

(1)利用已知函数的单调性,即转化为已知函数的和、差或复合函数,求单调区间.

(2)定义法:先求定义域,再利用单调性的定义.

(3)图象法:如果f(x)是以图象形式给出的,或者f(x)的图象易作出,可由图象的直观性写出它的单调区间.

(4)导数法:利用导数取值的正负确定函数的单调区间.