gongzhong号,可在微信好友里自动收到每天的推送,还可以查看全部资源。
识别下面ErWeiMagongzhong号

七、八、九年级的童鞋们,每天都可以从这拿到一道数学题哦!知识强化、课外拓展、思维提升,都在这一道数学题里了。提醒大家:题目不简单,够胆来挑战!请认真答题,一定要坚持住哦!也欢迎邀请同学参与到我们的答题中哦!刷屏到文末,点击左下角“”可查看“7-9年级”全部课程。请同学们准确理解什么是同类项,并判断下列说法是否正确,正确的在横线里打“√”,错误的打“×”.
【答案】
×,√,√,×,√
【分析】
根据同类项的定义(所含字母相同,相同字母的指数相同),即可作出判断.
【解答】:(1)3x与3mx是同类项,所含字母不同,不是同类项;
(2)是同类项;
(3)是同类项;
(4)所含字母不同,不是同类项;
(5)是同类项.
故答案是:×,√,√,×,√.
已知:函数y=(m+1)x+2m﹣6
(1)若函数图象过(﹣1,2),求此函数的解析式.
(2)若函数图象与直线y=2x+5平行,求其函数的解析式.
(3)求满足(2)条件的直线与直线y=﹣3x+1的交点.
【答案】
【分析】
(1)根据一次函数图象上点的坐标特征,把(﹣1,2)代入y=(m+1)x+2m﹣6求出m的值即可得到一次函数解析式;
(2)根据两直线平行的问题得到m+1=2,解出m=1,从而可确定一次函数解析式.
(3)两直线的解析式联立方程,解方程即可求得.
【解答】:(1)把(﹣1,2)代入y=(m+1)x+2m﹣6得﹣(m+1)+2m﹣6=2,
解得m=9,
所以一次函数解析式为y=10x+12;
(2)因为函数y=(m+1)x+2m﹣6的图象与直线y=2x+5平行,
所以m+1=2,解得m=1,
所以一次函数解析式为y=2x﹣4.
(3)解 得
得 ,
,
∴两直线的交点为(1,﹣2).
【点评】本题考查了两直线相交或平行的问题:两条直线的交点坐标,就是由这两条直线相对应的一次函数表达式所组成的二元一次方程组的解;若两条直线是平行的关系,那么他们的自变量系数相同,即k值相同.
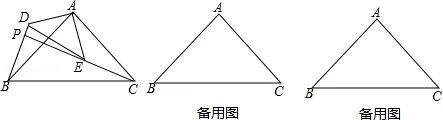
如图,△ABC和△ADE是有公共顶点的等腰直角三角形,∠BAC=∠DAE=90°,点P为射线BD,CE的交点.(1)求证:BD=CE;
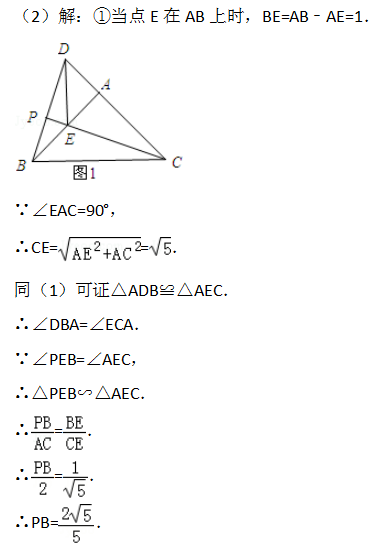
(2)若AB=2,AD=1,把△ADE绕点A旋转,当∠EAC=90°时,求PB的长;
【答案】
【考点】:
S9:相似三角形的判定与性质;KD:全等三角形的判定与性质;KW:等腰直角三角形;R2:旋转的性质.
【解答】:
(1)∵△ABC和△ADE是等腰直角三角形,∠BAC=∠DAE=90°,
∴AB=AC,AD=AE,∠DAB=∠CAE.
∴△ADB≌△AEC.
∴BD=CE.


——END——
来源:本文内容来源于网络,我们尊重原创,如有侵权联系删除。






相关资源