了解一些概率学思维,你的人生也许会大不同

发布于 2021-08-31 12:31 ，所属分类：中小学阅读学习资料

说起“概率思维”，其应用的基础是概率学原理，概率学，大至宇宙形成，小至垃圾邮件过滤几乎每件事都有它的身影。

有人说，万事万物都离不开概率，就像我们也在无时不刻也都在做着选择，怎样才能使预期的成功率达到最大化？这就需要我们了解一些概率学的知识了。

我们先来做个小测试~

印度文学教授，还是细胞生物学家？

请大家阅读以下描述之后回答问题~

有一位叫尼赫鲁的教授在一所美国大学里面任教，他精通梵文，并且订阅了《印度文化》这个期刊；他还有每天晚上写诗的习惯，收集佛像也是他的爱好之一。

你觉得尼赫鲁教授，更可能是一个印度文学教授呢，还是一个细胞生物学家？

绝大多数人应该都会觉得，他应该是一个印度文学教授，因为他身上的这些特质太符合一个印度文学教授的特质了。

不然的话，能有几个细胞生物学家会精通梵文呢？又有几个细胞生物学家会回到家之后去写诗、去收集佛像呢？

但事实上，如果你猜他是一个细胞生物学家，你猜对的概率会更高。

那为什么会这样呢？

其实道理很简单，因为在整个美国，只有100个印度文学教授，但是却有50000个细胞生物学家，这就是基础概率。

虽然尼赫鲁教授的特征，和印度文学教授的特征匹配度高达90%，而与细胞生物学家的特征匹配度只有5%，但是，当你把这个匹配度乘以刚才说的基础概率之后，你就会发现：尼赫鲁教授是细胞生物学家的概率，会是印度文学教授概率的2.7倍。

这就是我们经常容易犯的一个错误，叫做忽略基础概率。

而概率，就是要帮助我们了解不确定性，在数学领域中，概率论是专门研究“可能性”的一个分支。它涉及的问题非常广泛，涵盖的内容远远超过课本里的知识。

一切随机或者不确定的事件，都是概率论研究的范畴。上至气象下至金融，甚至连“磁铁的磁性是怎么来的”这种物理问题，都可以用概率的方法进行研究。

概率论起源

不过，虽然概率论的应用范围非常广泛，但这门学科的诞生却有些“不太光彩”。

1654年的一天早上，法国数学家布莱兹·帕斯卡收到了他的朋友贡博的一封来信。

这位朋友向帕斯卡提出了如下问题：

两位贵族A与B正在进行一场赌局，赌注是每人500法郎。游戏规则很简单，两人轮流掷硬币，得到正面则A得一分，反面则B得一分，每局两人得分的机会相等，谁先得到6分谁就拿走这1000法郎。两人激战至2比4之际，B突然有事需要提前终止赌局。

那么究竟应该如何分配赌资才最公平呢？

作为一代数学大家，帕斯卡对此也产生了浓厚的兴趣。随即，他便向另一位业余数学家皮埃尔·德·费马发去了一封信，共同讨论这个问题。

“业余数学家之王”费马很快就给出了一个答案。他认为，不能单凭赌局停止时的比分或者各自获胜所需要的分数来决定赌注的分配，而是应该考虑所有比赛可能出现的状况，从而计算出双方的获胜比例。

实际上，他们的解答就相当于在计算两位玩家胜利概率的大小。在研究中，帕斯卡提出了“数学期望”的概念，以及著名的“帕斯卡三角形”。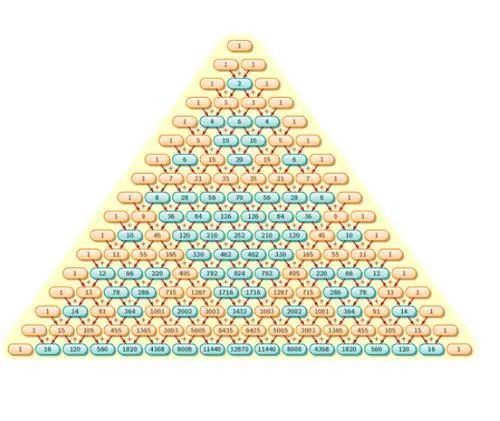

某个结果为实数的随机事件的数学期望，也就是所有结果按照发生概率加权之后的平均值。

数学期望这个概念，掀开了概率论研究的序幕。

概率学的发展

很多概率问题都有着特别的结构。以某个非常简单的随机事件来说，比如抛掷硬币。

我们知道每种结果出现的可能性的大小，而这类事件就被称为“基本事件”。我们可以多次重复这些基本事件，假定它们发生的可能性不会改变，而且这些重复没有相互影响。

如果我们将这些基本事件以合适的形式组合起来，就能得到一个更为复杂而有趣的系统。

这样构成的随机系统就被称为古典概型。

如果让数学家评选概率论中最重要的定理，那么桂冠非“中心极限定理”莫属。它不仅是概率论中许多重要结果的基石，也是支撑众多行业发展的顶梁柱。

假设我们有一枚硬币，它掷出正反面的概率相等，那么，如果我们连续抛掷这枚硬币一万次，常识告诉我们，其中为正面的结果大概是五千次，这就是大数定理。

而中心极限定理则告诉了我们额外的一点：如果将许多相同而又独立的基本事件的结果取平均值的话，这个概率分布必定是一个所谓的“正态分布”，其结论是基本事件越多，平均值的不确定性就越小。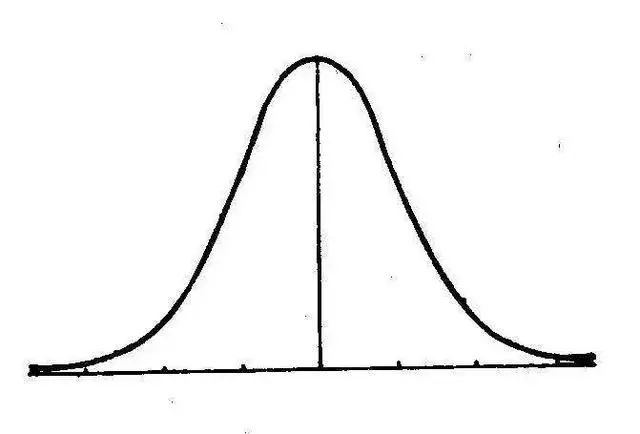

也许你很难想象，中心极限定理也是保险整个行业的基础。我们每个人都会遇到各种各样的风险，比如事故、疾病等等。

虽然这些风险发生的概率都很低，可一旦发生，其后果将非常严重，并非每个人都能承受。

而保险业正是基于这一点，通过保费与保险赔付的方式，将上千万人连接了起来——每个人都只付出相对小的代价，但在不幸袭来时，就能获得一定的保障。

根据中心极限定理，我们可以得知，由数量庞大的个案相加而成的保险业务，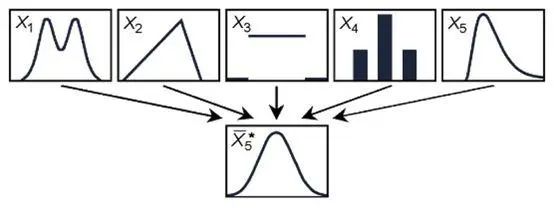

除了与不确定性相关的问题之外，概率论与物理也有着千丝万缕的联系。

法国物理学家皮埃尔·居里（居里夫人的老公）在攻读博士学位时，就发现了一个关于磁铁的有趣性质：无论磁力多强的铁制磁铁，在将其加热到770℃时，都会突然失去磁性。

这个温度后来就被称为铁的居里点。那么，为什么磁铁会突然失去磁性？通过概率论与统计物理分析，我们现在明白，这种现象与冰雪消融、开水沸腾类似，都属于相变的范畴。

我们可以将磁铁里的铁原子想象成一个又一个的小磁针，在磁铁还有磁性时，这些小磁针都会齐刷刷地指向同一个方向。但因为分子热运动的关系，每个小磁针都会时不时地动一下，但很快就会被附近的小磁针重新同化。

物理学家将这个场景抽象成所谓的伊辛模型。

通过对伊辛模型的研究，概率学家发现，当温度达到某个临界值时，整个体系就会由于热运动而不能保持统一的指向，这也意味着磁铁失去了磁性。

相变不仅仅局限于物理现象。流言的传播、传染病的爆发，还有微博的转发，都是一种相变过程，都存在着某种临界值。

例如在“三人成虎”这个成语中，“三”就是所谓的临界值。

又比如说传染病，在适当的模型下，如果每个病人传染人数的平均值低于某个临界值时，那么疾病就能被控制；如果高于临界值，就很可能导致疾病的全面爆发。

虽然对于疾病传播的研究，属于流行病学研究的范畴，但在概率论被引入流行病学研究之后，我们对如何防止与控制疫病爆发有了更深入的了解，这是能够挽救成千上万人性命的知识。

当然，概率论的应用远不止这些。大至失事飞机搜救，小至垃圾邮件过滤，我们都能在其中找到概率论的身影。这个复杂的世界充满了不确定性，有些无伤大雅，有些却能致命。若要驾驭这些不确定性，就要先从了解它们开始，这就是概率论的意义。

概率论不能为我们带来一个没有风险的世界，但它却能教会我们如何与风险和平共处，虽然它带来的仅仅是一种关于不确定性的知识。

课题推荐

来自威廉玛丽学院数学系教授的Prof.Clare将会给我们带来《概率论原理及其应用》。

对数学/应用数学/统计学等领域感兴趣的同学千万千万不要错过！

如何找到赢得扑克游戏的最佳策略；如何监控股票市场在适当的时间进行投资；如何预测天气变化；如何分析基因突变？上述所有问题，它们共同具有一个特点，它们都与随机性发挥重要作用的情况有关。我们为什么要研究概率论呢？概率论是研究随机现象的重要工具，更详细地说，概率论与统计学有关，在物理学、工程学、经济学、数据科学等领域有着广泛的应用，这对于打算在美国大学学习的学生来说是一个特别重要的课题。